Classical Theories – Special Relativity

Present article is the 4th one in a series, which continues from the 3rd: Perceptions of Physical Reality/ Classical Theories - Forces cited here as [III]; which together with the articles cited, [I] and [II], should be checked for explanations of some of the concepts appearing here. In [III], I had discussed the fundamental forces that determine the particle trajectories together with the related physical observables in the framework of the non-relativistic classical mechanics, i.e., the Newton-Galilean mechanics. The concept of forces developed into the concept of force fields. The gravitational field stood all alone but the electric and magnetic fields were unified in the form of electromagnetic fields with the associated phenomenon of electromagnetic waves. Light was recognized to be the electromagnetic waves. Consequent developments forced upon us some radical adjustments to the earlier concepts of space and time, which were thought of as the absolute independent entities. This necessitated in turn some adjustments to the earlier formulations. The pertaining issues are discussed in the present article.

History of Special Relativity

It is normally assumed that the special theory of relativity was developed in its entirety by Einstein. In fact there were many contributors to the development of this theory over a period of time, most notable ones being Lorentz and Poincare. It has been said that in view of the earlier developments, the final form of the special theory of relativity was to be an immediate natural outcome. Here we mention briefly some developments preceding and about the time of Einstein’s formulation.

It was pointed out in [III] that waves need a medium to propagate. Aether, spelled also as ether, was assumed to be such a medium for the propagation of the electromagnetic waves. Lorentz in 1892 assumed the existence of electron and modified the Maxwell-Hertz equations to Maxwell-Lorentz equations, still referred to as Maxwell’s equations. Aether in his theory is at absolute rest. Efforts at finding a reference frame at absolute rest were still continuing. If such a frame did exist, it could be taken for the absolute, preferred frame of reference for the formulations of the laws of physics and thus, disprove the Galilean relativity principle. Lorentz also introduced the concept of local time, which intertwined the time and space. While the local time was a mathematical tool to Lorentz, it was Poincare who recognized in 1900 that the local time was actually the time indicated by the moving clocks and thus, eliminated the independent absolute nature of time and space.

With some contributions by Larmor, Lorentz also deduced his transformations differing from Galileo’s. According to Galileo’s transformation rules, a frame moving, say at 100 m/sec, after one second would be 100 m away from an observer at rest but only 25 m away from an observer chasing it at 75 m/sec. Measuring rods are the same length and the ticking rates of the clocks are the same in both reference frames. According to Lorentz transformation, this 25 m would be further adjusted by a multiplicative factor as the moving measuring rods contract and the moving clocks slow down. The contraction factor depends on the velocity of the frame. Similar rule for the time transformation already developed in part by Poincare was adjusted for such a contraction. These are now called the Lorentz transformations. Space and time in these rules are intertwined, becoming coordinates of a four dimensional space-time. Poincare studied these transformations in detail. If these rules are adopted, then Maxwell’s equations remain the same in all inertial frames of reference. This issue will be revisited in this article.

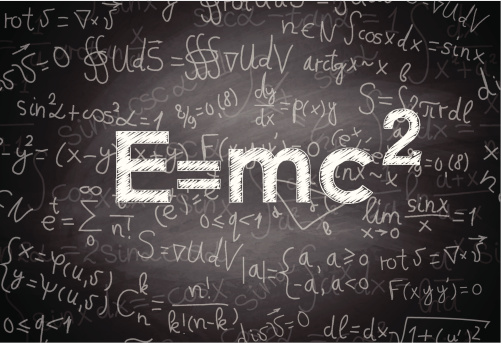
During the same period, Thomson, FitzGerald, Heaviside and Searle recognized that an electromagnetic field has energy and mass, and determined that the energy is directly proportional to the mass multiplied by the squared velocity of light, a precursor to the famous relativistic mass energy equivalence relation E = mc², which was derived by Poincare in its exact form. There were several other physicists, particularly Hasenohrl who deduced similar relations. Kaufmann verified mass-energy equivalence around 1901-1903. Einstein deduced this relation together with the Lorentz transformations in 1905. Max Born commented at Einstein for failing to recognize the earlier contributions.

Yet again, some physicists, e.g., Ernst Mach had suggested in about 1883 that absolute space and time are meaningless and only the relative motion is a useful concept. Poincare argued that a violation of the relativity principle can never be detected. Michelson-Morley experiments designed to detect the motion of Earth in aether produced negative result thereby disproving an existence of aether. Thus, Galileo’s principle of relativity remains intact.

The periods during which Poincare’s and Einstein’s work on relativity appeared overlap; thus they could not cite each other; and it is understood that they developed the special theory of relativity in its “final form” independently. While there are differences in the exposures, the theory is essentially the same. The earlier developments concentrated on the electromagnetic fields; Poincare and Einstein widened its scope to some extent, which was completed later. Full incorporation of mechanics in this theory took some more time. It should be remarked that while Poincare formulated and studied the concepts in a mathematically sound framework, casting certain concepts in the framework of the Poincare groups, Einstein’s initial work lacked such rigor. His work was later reformulated by Minkowski in a mathematically sound framework on the background of the Minkowski manifold, which provides the space-time structure underlying the special theory of relativity. It is said that after Minkowski’s reformulation, Einstein commented: “Now, I don’t understand my own theory.”

Development of the theory of relativity was also tainted by the international political situations, including the racial and racist hues, of the day, drawing media’s attention bringing some sensationalism with it. Skipping all that, I mention a couple of misconceptions created in the process. One misconception was created by a cartoon in which Einstein supposedly explains the concept of time dilatation by stating that the time passes slowly if one is sitting on hot iron but very fast if one, presumably a man, is chatting with a pretty woman; thus creating an impression that time dilation is psychological, while in reality it is physical: Moving clocks slow down. Same is the case with the moving rods, mathematical line segments, which shrink in the direction of their motion. The second misconception purports that only a few people understood the theory of relativity. It is said that when a reporter asked Eddington if it was true that only three individuals understood the relativity theory, Eddington commented, “Who is the third one.” According to another rumor, only about a dozen people understood it. In reality, the special theory of relativity was almost here about the time Poincare and Einstein developed its final formulations and its basic elements including about all results, can be explained to the high school students. Admittedly, there are complex mathematical structures built around it as is the case with about all formulations but they do not constitute any basic crucial part of the theory; they provide further deeper understanding mostly to mathematically oriented physicists.

The historical development of the theory and the controversies of any kind surrounding it are rather inconsequential as far as its conceptual structure is concerned, which is our main concern that I will attempt to describe below. The exposure is based on the standard Einstein-Minkowski formulation.

Lorentz Transformations

Einstein’s formulation is founded upon two basic postulates, i.e., assumptions, axioms. The first assumption is that all inertial frames of reference are equivalent for the formulation of the laws of physics, i.e., the Galilean principle of relativity is valid. The second assumption is that the velocity of light in vacuum is the same in all inertial frames of reference. Einstein called the second assumption “only seemingly at variance with the first.”

Consider again the example of the three frames of reference discussed above, i.e., frame “A” moving at 100 m/sec. and “B” moving at 75 m/sec. with respect to “G,” the frame at rest with respect to the ground. According to the Galilean transformation rules, “A” moves with a velocity of 25 m/sec with respect to “B.” Now, let “A” be attached to the light, which moves with a very large velocity denoted by c, equal to about 3x10⁸ m/sec. According to the second postulate, “A” moves with the same velocity, c, with respect to “G” as well as with respect to “B.”

It is clear that in the special theory of relativity the frame attached to light is singled out; it does not abide by the same rules as the other frames; and thus, is clearly not equivalent to the other inertial frames of reference. Consequently, the second postulate is at variance with the first, i.e., with the Galileo’s principle of relativity, not just seemingly at variance and is now universally considered to be so. This violates the basic premise of the physical theories that they should be founded upon a self-consistent set of assumptions.

The two postulates of relativity theory exist in an uneasy coexistence essentially because the resulting formulation describes the nature splendidly well within its range of applicability. Another major continuing concern about the second postulate is that even though some earlier suggestions were made to this effect, its justification remains the fact that this is an experimental fact. As indicated in [I], making the experimental facts into the assumptions of a physical theory are not looked upon favorably for they introduce an element of empiricism in the theory. Einstein had defended this objection by insisting that carefully selected experimental facts can constitute legitimate founding assumptions of the theories, which came to haunt him when he objected to Heisenberg’s inclusion of his uncertainty principle on the experimental grounds.

It is abundantly clear that the results of the special theory of relativity are “correct” even though some questions about its foundations remain unresolved. Such formulations constitute legitimate interim theories. Improving the existing theories and replacing them with more tenable ones is a continuing process. In case of the relativity theory, attempts at deducing the results of the special theory of relativity without the second postulate or by replacing it with some more tenable assumptions are still continuing and not without some success.

To accommodate this peculiar property of light, it became necessary to make adjustments to the Newton-Galilean formulation. The requirement that the velocity of light remains the same in all inertial frames yields the Lorentz transformations, which place the space and time on equal footing; time assumed the character of the fourth dimension, just like the space dimensions. According to the Galilean transformation rules, the coordinates of a location in frame “B” at a given time are given by the coordinates in “G” minus the distance travelled by “B” during that time. According to the Lorentz transformations, this number is altered by a multiplicative Lorentz factor depending on the velocity of “B,” which is equivalent to the fact that the measuring rod in “B” looked upon from “G” are shorter than in “G;” the shrinkage depends on the velocity of “B.” Similarly, the time of an event lapsed in “B” is calculated in “G” by subtracting an amount of time from the time lapsed in “G,” which requires a more complicated calculation than for the location, which is adjusted further by the same multiplicative factor as for the location. This amounts to the fact that the ticking rates of clocks in “B” observed from “G” are slower than in “G.” It should be mentioned that this derivation does not assign a preferred status to “G.” The same rules apply if we take “B” to be at rest and “G” to be moving with respect to it. Thus, to an observer in “G,” the clocks in “B” are slower; and to an observer in “B,” the clocks in “G” are slower; and so forth.

The result that the clocks slow down in a moving frame with respect to the one at rest, created a paradox, known as the Twin Paradox. In this scenario, Joe and Moe are the twins. At the time of their birth, Joe takes a space ship and travels at a high speed while Moe stays on the Earth. Joe returns many years later. By then Moe is an old man and to him, Joe is still young. The situation reverses for Joe for it is Moe who is travelling with respect to him. This paradox is still debated but it is based on a fallacy for the following: Joe must accelerate at the time of birth in order to acquire a velocity and decelerate upon return to come to rest on the Earth for a legitimate comparison; and an accelerated frame of reference is not inertial. The rules of the Lorentz transformation apply to the inertial frames of reference only. Lorentz contractions have been abundantly verified experimentally. An example of the time dilatation is provided by the fact that some particles with a life span of a miniscule fraction of a second at low velocities survive longer if moving with higher velocities and the life span conforms to the Lorentz contraction rules. Relativistic formulation is now quite basic to the theories of the physical phenomena.

Relativistic Spacetime

The Lorentz transformations introduce a new measure of invariant “length” in the four dimensional spacetime. For convenience, we use the natural units in which the velocity of light assumes value equal to one. In natural units, the square of this “length,” called the “Proper Time,” between two events is equal to the squared time difference between the events minus the squared special distance between the locations of the events, which can be positive, negative or zero.

In view of the Lorentz transformations, the proper time for the light is equal to zero, which is the converse of the process used to deduce the transformations, i.e., setting the proper time for light equal to zero yields the Lorentz transformations. Furthermore, squared proper time separating the two events is invariant, i.e., it is the same in all inertial frames, even when it is not zero, i.e., for the material particles. This measure of the invariant length is sufficient to endow spacetime with the Minkowskian structure, which is sufficient to deduce the Lorentz transformations and of course the invariance of the velocity of light. For this reason, some authors deduce the results of the special relativity from the single assumption of the validity of the Lorentz transformations or the Minkowski structure of spacetime. However, this only camouflages the assumption of the invariance of the velocity of light, not eliminate it.

Squared proper time involves a subtraction that is responsible for endowing the spacetime with the Minkowskian structure, which differs in a fundamental way from the Euclidean structure of the three-dimensional space where the length squared is the sum of the three squared coordinate differences. Introduction of a Minkowskian structure in spacetime, which describes the relativistic formulation in a more satisfactory way than the original, is more in accordance with the view of Leibnitz, among others, that the structure of spacetime is not absolute; instead it is “mental,” i.e., mathematical, which is a product of the mind; constructed to describe the perceived reality.

Instead of introducing the Minkowskian structure, one can take the time to be an imaginary dimension and use the rules of the Euclidean geometry, to obtain the same results. This does not mean that time dimension is imagined; it is as real as the space dimensions. In mathematics imaginary numbers were introduced as the square roots of negative numbers, i.e., an imaginary number squared is a negative number. These numbers play a significant role in electromagnetism as well as in other areas of physics. In the electromagnetic instrumentation, workings of the gadgets like the electric motors and generators are described in terms of the intertwined real and imaginary numbers, called the complex numbers. In view of the fact that the squares of imaginary numbers are negative, it is easy to see how the same results can be obtained by taking the time as an imaginary dimension and using the rules of the Euclidean geometry as by introducing the Minkowskian structure in spacetime. However, the later is more satisfactory for various reasons.

Light Cone and Causality

The Minkowskian structure defines two regions in the spacetime separated by the surface of the light cone, which is actually two cones joined at their common vertex, as shown in the figure below. The surface of the composite cone defines the path of light. Points in the interior of the cone describe the motion at speeds less than that of light and the points in the exterior describe the motion at speeds more than that of light.

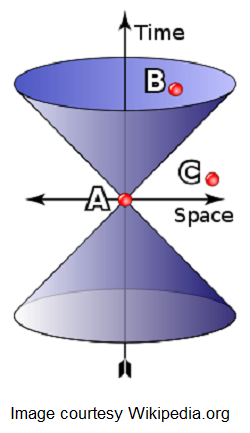In this figure, the interval “AB” is “time-like”; i.e., the squared proper time between the events “A” and “B” is positive; e.g., for a particle traveling at speeds less than that of light, the proper time would be positive. In this case, there is a frame of reference in which the events “A” and “B” occur at the same location in space but at different times. “A” precedes “B” in that frame, and in all inertial frames. Consequently, there can be a causal relationship between the two events, with “A” the cause and “B” the effect. Intervals on the surface of the cone relate only to the propagation at speeds of light, i.e., the travel time of light is equal to the time-separation of the events. The interval “AC” in the diagram is “space-like,” defined by the negative squared proper time, i.e., the events take place in faster succession than the light would take to travel between the locations of the events. In this case there is a frame of reference in which events “A” and “C” occur simultaneously, separated only in space. There are also frames in which “A” precedes “C” as shown, and frames in which “C” precedes “A.” In this case, the paradoxes of causality would result, which is discussed below. The paradoxes occur essentially because the events take place faster than the travel time of light between the events.

To fully understand the above assertions and the paradoxes, some algebraic manipulations are required, which we must omit. Thought experiments were conjured up by Einstein and Tolman for space-like intervals, i.e., if a signal or a body could travel faster than the light, in which the effect could precede the cause, which violate the causality. They concluded that this constitutes no logical contradiction but it contradicts the totality of our experience so that the impossibility of travel faster than light is “sufficiently proven.”

A logical contradiction does result in a thought experiment. Suppose Alice is on a spacecraft moving away from the Earth and she wants to communicate with Bob back home. Assume that both of them have devices that are capable of transmitting and receiving faster than light signals. It can be shown that this way a signal can reach one before it is sent by the other, say one hour before. Now, they reach an agreement that Alice would send a message to Bob at three o'clock if and only if she does not receive one from him at one o'clock. Bob sends a message to reach Alice at one o'clock immediately upon receiving one from Alice at two o'clock sent by Alice at three o’clock. Then the exchange of messages will take place if and only if it does not take place. This is a genuine logical causal contradiction.

Some credible research has indicated that the concept of causality goes as far back as the natural philosophy developed in the Samkhya, Vaishashika and Nyaya systems of Hinduism and it was pursued, and assigned a paramount importance in the Karma Yoga philosophy. Furthermore, it was asserted that this doctrine made its way from there into more recent physics. The concept of causality is so sacred to the physicists that in view of the inconsistency resulting from a causality violation, it was concluded that the superluminal particles such as the tachyons cannot exist. However, there are physicists, mainly Sudarshan, who maintain that tachyons can and do exist. To circumvent the problem of the causality violation, ways have been proposed to possibly remove such inconsistent results, which required some later developments.

Time

In the Newton-Galilean formulation, time was assumed to be an absolute independent parameter. In the relativistic, Minkowskian formulation, time is just another independent dimension as is each one of the space dimensions. While the detailed description of a recent development that may alter our view of the time, and thus of spacetime radically, is beyond the scope of the present article, its brief discussion would be valuable for its significance in the present context. This development might be revisited in a later article. First we discuss some background issues.

Euclid placed the three-dimensional space perceived as “natural” on precise axiomatic foundation. One of the axioms states that through a point outside a straight line, one and only one line parallel to the original one can be drawn. Attempts were made to deduce this axiom from the others, which remained unsuccessful. It was realized in time that the axiom of the parallel straight lines is an independent necessary ingredient for the construction of the Euclidean geometry. As indicated in [I], mathematics is an art that has nothing to do with reality. Mathematicians often amuse themselves by playing with the existing mathematical structures or by constructing new ones out of their minds. It is said that Leonardo da Vinci, would suddenly take a break from his scientific lab and go to his painting studio just to put a few minor strokes to the smile of Mona Lisa to improve it. This activity continued for years. Similarly, mathematicians put some minor “strokes” to the existing mathematical structures at times just to see what kind of a new structure comes out of it. Riemann decided to remove the axiom of the parallel lines from Euclid’s axioms to see what kind of geometry would result. Thus came to be the beautiful Riemannian geometry. Later, this geometry provided the underlying geometry for the general theory of relativity to be discussed in a later article. Not just the general relativity, the Riemannian geometry underlies most of the modern physical theories of particles and fields.

There have been other mathematical systems created by the mathematicians to go the same route as the Riemannian geometry. I mention one more: After the theory of the Lie groups was completed by Sophus Lie, which too is a geometrical system, mathematicians boasted that finally they had created a purely mathematical system, which has nothing to do with reality. Now the Lie groups provide a crucial component for the structure to formulate the modern theories in physics. In fact, this structure underlying the modern theories of particles and fields is constructed by its complementary constituents of the Riemannian geometry and the Lie groups.

To put it in perspective: A perception of reality developed with some help from the experimental observations, that of the special relativity, was cast in the framework of the Minkowskian structure by placing the time at par with the space coordinates, just by extending the definition of the “length.” The Riemannian geometry was constructed by removing the parallel lines axiom of the Euclidean geometry, which went on to become a crucial element contributing to our perceptions of reality. The theory of the Lie groups that was developed just by pursuing the operation of multiplication, which is all too familiar for the real numbers, to its extreme, went on to join hands with the Riemannian geometry to define a perception of reality. Frequent occurrences of this type make one think again: Does reality have an existence of its own or it is just the constructs of mind that we cast our experiences pertaining to the workings of nature in, to develop our perceptions of reality. By creating the perceptions of reality with our minds, do we “create” reality for what else is reality if not what we perceive of it?

In the same vein, let us amuse ourselves by constructing a structure out of the three-dimensional Euclidean space. A straight line segment and thus, its arclength is determined solely by the two end points of the segment. The line can be parameterized by the arclength measured from an arbitrarily selected reference point, by associating the three spatial coordinates of a point with the arclength covered up to that point. There is no need to introduce any external parameter for this purpose. This is done routinely in mathematics inducing the same in physics also. Now, we can construct a graph by plotting the coordinates with respect to the arclength, the parameter; again a standard practice to place a formulation in a more discernible, visual form. What results is the surface of a cone; in fact two cones, one being the reflected image of the other. The surface of the cone defines its interior also, which corresponds to the non-straight lines. The exterior is also naturally determined. This cone is exactly like the light cone, prompting one to identify the arclength with time. With this identification, the construction yields the light cone in the natural units. Thus, we have constructed the Minkowskian manifold from purely mathematical considerations providing the basic geometrical structure to formulate our pertaining experiences leading to the theory of special relativity in its completeness. With some further developments, this concept has been shown to provide also a formulation of the electromagnetic fields founded upon radically different axioms than the previous ones. This formulation admits further natural extensions.

This, above, construction would have a profound impact on our perception of the time and thus of the spacetime, for as its consequence, the time is identifiable with the arclength of the totality of curves in the Euclidean space. In view of this, the time would lose its fundamental character as it would be deducible solely from the elements of the three dimensional Euclidean space, and the spacetime structure would become the result of a natural logical mental construct out of the three-dimensional Euclidean space as perceived by us naturally. However, once the time is available, even if constructed purely out of the Euclidean geometry, other discussion pertaining to the special relativity, and wherever else the time is needed, remains the same.

Mass-Energy Equivalence

In the pre-relativistic mechanics, time served as an independent invariant parameter to describe the evolution of physical systems, e.g., the motion of a particle. In the relativistic mechanics, time assumes the role of the fourth dimension of the four-dimensional spacetime complex, playing a role similar to each of the three space dimensions. Therefore, we need some other parameter to describe the evolution of physical systems in the relativistic setting. The proper time, which is an invariant of the relativistic formulation, tends to the time as the particle velocity tends to zero. Thus, proper time is a suitable, in fact a natural, extension of time to serve as the evolution parameter.


With proper time as the parameter, the velocities are defined anew as the rates of displacements with respect to the proper time. A new velocity appears naturally, which is the rate of change of time with respect to the proper time. The extended four-dimensional velocity vector is Lorentz covariant. In the pre-relativistic mechanics, a particle’s momentum, defined to be the velocity multiplied by its mass, was described by its three components, corresponding to each spatial direction. The definition of momentum need be extended to conform to the Minkowskian structure of spacetime also, i.e., the momentum must have four components transforming in accordance with the Lorentz transformation rules as opposed to the earlier Galilean transformations. The new momentum vector is defined to be the generalized velocity vector multiplied by the mass of particle. Three space components are thus replaced by a “mass” multiplied by the non-relativistic velocity. Since the proper time is less than the time, this new mass is higher than the non-relativistic mass depending on the velocity of particle. This mass is now called the “mass” of particle and the non-relativistic mass is called the rest mass, since the mass for the velocity equal to zero, i.e., for a particle at rest, is equal to the non-relativistic mass. As for the velocities, there appears a new component of the momentum, the fourth momentum. The extended momentum vector is a Lorentz covariant vector, i.e., it is a vector in the underlying Minkowski space.

In addition to the velocity and momentum, other physical quantities, e.g., the force, are extended to the Minkowski manifold. With these extensions, Newton’s laws and the action principle admit natural Lorentz covariant extensions and the relativistic mechanics is developed out of the non-relativistic one in a natural way. Maxwell’s equations were known to be Lorentz covariant, which had stimulated early developments of the relativistic formulation. However, the formulation of electromagnetism was also streamlined by introducing the concept of the electromagnetic potentials constituting the components of a Lorentz covariant four-vector. The electromagnetic fields then assume a secondary role of the deduced quantities. The potentials also arise naturally in formulating the mechanics of a charged particle in an electromagnetic field in the framework of the action principle.

As the velocity of a particle increases, its mass increases and thus, its inertia to force increases; i.e., particle’s inertial mass increases; it takes more force to produce the same acceleration at higher velocities than at the lower velocities. Since the proper time tends to zero as the velocity of a particle tends to the velocity of light, the mass of a particle tends to infinity, requiring about infinite amount of force to accelerate it. Thus a material particle, i.e., with non-zero rest mass, can never achieve the velocity of light, and thus cannot exceed it. This conforms to the causality principle. Mathematically, parallel results apply to the tachyons, which if they exist, cannot be slowed down to the speed of light and below.

The notion of the conserved quantities has played a significant role in physics. In particular, the energy is understood to be conserved in all physical systems. For example, heat, which is energy, could be generated by work, e.g., by rubbing two material bodies against each other. Thus, heat does not conserve in this process. So, the definition of energy was extended to consider the work and heat just two forms of energy. In this process, the work is converted into heat and the conservation of energy principle holds. A heat engine, e.g., the steam engine, converts heat into work. Similarly, all forms of energy can be converted into each other, e.g., the gravitational energy is converted into the electromagnetic by hydroelectric generators. Considering all forms of energy equivalent, it was made into a law, the first law of thermodynamics: Energy can neither be created nor destroyed. This law was developed before some forms of energy were even discovered but it survived intact with adjustments to the concept of energy as needed.

A fruit on a tree has potential energy due to the gravitation in the sense that when the fruit breaks away from the branch it falls to the ground and acquires the kinetic energy; the potential energy is converted into the kinetic energy. The total energy along its trajectory, which is the sum of the potential and the kinetic energies, remains constant at every point of its trajectory; total energy is conserved even though each of the two forms does not conserve by itself. Realized or potential kinetic energy came to be the basis of all forms of energy.

The fourth component of the relativistic momentum constitutes a component of a Lorentz covariant four-vector and it is a conserved quantity as are the other components. In the natural units we are using, it is equal to the relativistic mass of the particle, which for the low velocities  is about equal to the sum of the rest mass of particle and its non-relativistic kinetic energy. In the non-relativistic setting, which is quite accurate for low velocities, the kinetic energy is a conserved quantity. The relativistic effects become noticeable at high velocities. The correct value of kinetic energy results if all effects are included. In the relativistic setting, neither the conventional non-relativistic kinetic energy, applicable at low velocity, is a conserved quantity, nor is the fourth momentum minus the rest mass, which is the total kinetic energy. To retain the law of conservation of energy, the definition of energy was adjusted, which is now equal to the fourth momentum. This is equal to the relativistic mass in the natural units we are using. In the standard units, it is equal to the relativistic mass multiplied by the squared light velocity, yielding the famous mass-energy equivalence relation: E = mc². A particle at rest still has energy, called its rest energy. Except for the units, the mass of a particle and its energy define the same physical observable.

We have outlined the deduction of the mass-energy equivalence relation essentially by a mathematical reasoning. Historically, this equivalence relation was developed for the electromagnetic energy as it was noticed that a field increases the inertia of a charged particle. Later on the proofs were developed for the mechanical processes also. Experimental verifications of this relation followed. It is interesting to note that a purely mathematical reasoning led to an experimentally verifiable result, which was obtained by other methods also. This mass-energy equivalence constitutes the basic relation for calculating the energy released in various processes, most notable ones being the fission nuclear reactors and the fission based nuclear weapons.

Concluding Remarks

Newton’s laws introduced the concept of forces, which developed into the concept of fields, particularly the electromagnetic. Then the electromagnetic waves arose mainly out of the mathematical considerations, which were experimentally observed later. Seemingly unrelated entity, light was understood to be the electromagnetic waves; visible part covering a narrow range of frequencies. Need for a medium for waves to propagate forced upon us an untenable concept of aether, which forced us to choose between the Galilean relativity principle and the Newtonian concept of absolute space, preferred frame of reference. Experimental observation proved to be the arbiter in favor of the Galilean relativity principle. However, it left us with no medium for the electromagnetic waves to travel. For now, it was assumed that the electromagnetic waves could travel in vacuum as the fields can exist in the empty space and the electromagnetic waves are just the oscillating electromagnetic fields. This view would be superseded by yet another radical theory later.

To maintain the same form of Maxwell’s equations in all inertial frames in accordance with the Galilean principle of relativity required an alteration to the Galilean transformation rules leading to the Lorentz transformations and constancy of the speed of light that is at odds with the relativity principle. Yet again, it was an experimental observation, which settled the issue in favor of the constancy of the speed of light, which exists with the Galilean principle of relativity in an uneasy coexistence. Once the special theory of relativity was fully developed, our perceptions of the space and time were fundamentally altered; from independent absolute entities to entangled relative entities constituting the components of the four-dimensional Minkowski manifold. This in turn required that the moving measuring rods shrink and the moving clocks slow down. This also placed an upper limit to the achievable speeds. These consequences of the formulation were all experimentally verified. This was a major change in our earlier perceptions of the space-time complex. So far not widely known deduction of time from the three-dimensional space, presented in brief here, may alter this perception further.

Yet another major impact was on our perception of the mass and energy. Previously, the mass was understood to be essentially the invariant amount of matter in a body. A consequence of the relativistic formulation is that it is not so. The inertia to motion and hence the inertial mass increases with the increasing velocity. As a consequence, the mass and energy were now seen to be just two names for the same physical property of a material body and in fact of the fields and waves also. This realization proved to be of an immense fundamental and technological consequence.

The relativistic formulation altered our perceptions of the space-time and the workings of nature on the background of spacetime in a fundamentally radical way. The history of its development also illustrated a beautiful interplay between metaphysics together with the pertaining philosophy; theoretical physics with its basic requirement to describe nature with a set of self-consistent assumptions; experimental physics together with its power to arbitrate and mathematics together with its ability to lead to natural logical consequences that become part of our perceptions of physical reality. Such occurrences would take place in an even more profound manner in some later theories.

In spite of the fact that the relativistic formulation altered our views of the spacetime and the workings of nature in a radical way, the resulting theory still remains deterministic as was the pre-relativistic formulation.

Images (c) Gettyimages.com