Apr 26, 2024
Apr 26, 2024
Quantum Theories – Founding Developments

Image (c) Gettyimages.com
After providing an overview of the varying perceptions of physical reality from the early days to the present, I described the pertaining classical theories, from the time of Galileo to the end of classical era with geometrization of this perception, in several articles available here under the classification “Education.” Classical theories are deterministic and local presenting an absolute, objective view of reality in conformity with the intuitive urge and intellectual prejudice for a clean understanding of nature compatible with our day to day experiences. This view of reality suffered a severe blow due to some phenomena not observed before and the consequent development of the quantum theories, which is the topic of the next few articles.
The Quantum Concept
First phenomenon challenging the classical wisdom was the black body radiation, i.e., light, radiated by a black body in thermal equilibrium. A black body can be emulated by a hollow cavity with a tiny aperture in it. Therefore, this phenomenon is also called the cavity radiation. Such a body absorbs all incident radiation, which it reradiates in its own characteristic pattern. As discussed in the article: “Perceptions of physical reality: Classical Theories – Forces,” light is constituted of the electromagnetic waves transmitting energy continuously. According to the calculations based on the classical theory of electromagnetic radiation, the radiated energy density tends to infinite as the wavelength decreases to zero, i.e., as the frequency increases to infinite, which contradicts the observations. This is known as the ultraviolet catastrophe.
In the year 1900, Planck assumed, effectively, that light is radiated as packets of energy, i.e., discrete quanta, not as a continuous wave. The energy contained in each packet, i.e., quantum, is directly proportional to the frequency of wave. The constant of proportionality is equal to about 6.63 × 10-34 m2 kg / s, which is pathologically small in standard units that are comparable to the scale of our day to day experiences. Wave theory of the electromagnetic radiation was so well established by that time that to believe that light could be emitted as quanta, which are discrete particle-like entities, was very difficult. Planck himself considered this behavior to have been caused by some underlying physical phenomenon, not as an inherent property of light. In contradistinction, Einstein assumed this to be an intrinsic property of light and called its quanta the “photons.” Since the electromagnetic field was considered to be an infinite set of simple harmonic oscillators, this particle-like behavior of light amounted to be quantization of the field oscillators. Einstein assumed further that such quantization applied to the material oscillators also and calculated the heat capacity of the solids, which with Debye’s adjustments yielded the results in agreement with the observations, lending credence to the quantum concept. However, Planck remained unconvinced who, in a reference letter supporting Einstein’s job application, is known to have said that Einstein’s view that light is made of quanta should not be held against him for if we do not experiment with silly ideas, right ideas will never come.
Another phenomenon at variance with the classical expectations was the photoelectric effect: Electrons are emitted from certain material bodies by the light incident upon them. However, if the frequency of the incident light is below a threshold value, there are no ejected electrons no matter how high the intensity is, but even a low intensity light ejects the electrons if the frequency is above a threshold value. This establishes quite decisively that light is absorbed in discrete quanta. When the quantum energy is higher than the energy binding the electron to the body, it is ejected; otherwise not. The excess energy shows up as the kinetic energy of the ejected electron. If energy was absorbed continuously, any frequency radiation would be able to eject the electrons as the absorbed energy could be increased by increasing the intensity or by a longer exposure. Calculations based on the quantum concept agreed with the observed values.
Particle-like behavior of the photons was further demonstrated by Compton’s observation in a photon-electron collision. Compton scattered light from a graphite target to realize this collision. Based on the quantum assumption, the energy transferred to the electron in the collision should show up as a wavelength shift of photon, which it did in agreement with the calculation. Thus, quantization of light implying its particle nature was firmly established; but then, wave nature of light had also been firmly established. Since the two properties are mutually exclusive, an impasse was reached. This issue will be revisited. For now, we continue with further developments following the quantization of light.
Atomic Structure
Materials were known to be composed of tiny particles called atoms. Experiments, particularly Rutherford’s around 1911, in which he used alpha particles to probe the atoms of gold, showed that an electrically neutral atom has a positive charge concentrated in a small region of space termed the nucleus, surrounded by a negatively charged diffused cloud. Such a structure cannot be stable as oppositely charged material parts would fall into each other due to the attractive force between them. Taking a clue from the planetary motion, discussed in the article “Perceptions of physical reality: Classical Theories – Forces,” Rutherford surmised that the negatively charged particles, the electrons, constituting the diffused cloud, must be revolving around the nucleus. However, an accelerated charge radiates electromagnetic energy, and thus, the electrons would soon spiral into the nucleus, leading again to an unstable structure. Niels Bohr in 1913 supplemented Rutherford’s suggestion by postulating that each electrons is confined to a definite circular orbit without radiating with the orbits constituting a discrete set and an electron can only jump from one orbit to the other; radiation is emitted or absorbed when an electron jumps from one energy level to the other, as shown in Figure 1 below.
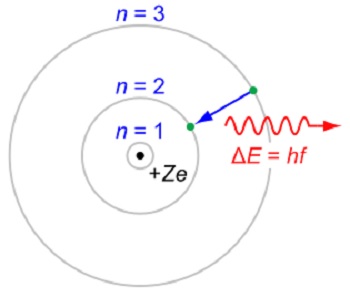
Figure 1. The Rutherford–Bohr model of the hydrogen-like ions
(Image courtesy Wikipedia)
In Figure 3, e is the electron charge; for hydrogen atom Z=1 and for hydrogen-like ions Z>1. An electron jump between orbits is accompanied by an emitted or absorbed amount of electromagnetic energy (hf), where h is Planck’s constant and f is the frequency of radiation. Shell radii characterized by the quantum number n were determined by matching the observed spectra of hydrogen-like ions. Clearly, this model conforms to Planck’s hypothesis that radiation is emitted and absorbed in discrete quanta of energy (hf). Later, Sommerfeld adjusted Bohr’s model by altering the orbits to the elliptical ones, in general, as in case of the planets. However, this adjustment does not add to our understanding in any meaningful way; therefore we ignore it for the present.
Bohr’s model of atom is essentially an empirical model devoid of metaphysical content. De Broglie suggested in 1924 that as the electromagnetic waves possess particle-like properties, material particles should be expected to possess wave-like properties, and thus introduced the concept of the matter waves. Thus, an electron must also be a wave. Now, if electron is a wave, then an electron orbiting a nucleus is a wave traveling along the orbit superposing upon itself. If after going around the orbit, the crest falls on the crest and trough on the trough, then there would be constructive interference creating a static wave with double the amplitude, which should yield a stable orbit. If crest falls on trough and trough on crest, then the wave would be neutralized; i.e., there would be no wave and thus an electron cannot exist in such an orbit. In between two such orbits, there would be a weaker wave with consequent low probability of electron being in such regions. Wavelength and the momentum of a matter wave were put in the same relation as they are for the electromagnetic waves, which were known from the work of Planck. Combining these relations, de Broglie deduced Bohr’s orbits. Initially, the concept of matter waves was dubbed “La comedie francaise (French comedy),” but it was here to stay for it was firmly established by further experimental observations, particularly the Davisson-Germer experiment, which is essentially a double slit experiment.
The observations in the double-slit experiment have played a crucial role in the above and later developments pertaining to the fundamental structure of quantum mechanics. We describe this experiment here together with the observations indicating their implications pertaining to the above conclusions.
Double Slit Experiment
Figure 2 shows the schematic of the double slit experiment together with the expected behavior of particles in the experiment on the basis of the pertaining classical understanding.
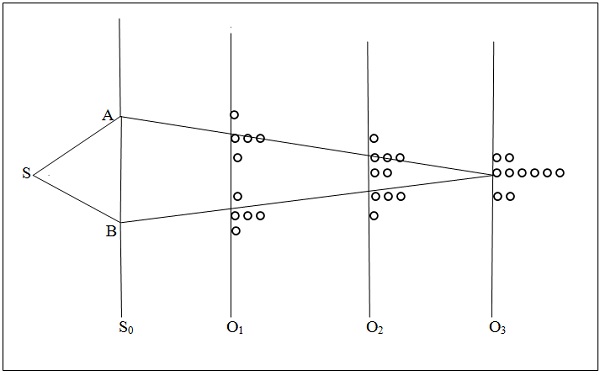
Figure 2. Double slit experiment with classical particles
In Figure 2, S is a source of the photons, electrons or any other entities, which encounter the screen S0 with two slits A and B, hence the name double slit. O1, O2 and O3 are the observation screens each one for one set of observations and the circles denote the entities observed. Location of all arrivals is about the same on a screen, shown separated for clarity. The observations shown are as expected if the entities are particles and the classical description of the particle motion is correct. Classically, the particles are deflected at the slits and travel along straight lines as shown. What is observed depends also on the location of the observation screen. After many of the particles have arrived, then at the location of O1 there would be two separated density regions; on O2, the two regions overlap partially forming a high density region with a dip in the middle; and on O3, they overlap fully forming a high density region. Number of particles on a screen is just the sum of particles coming from each slit. In principle, the particles should travel along straight lines landing precisely at the corresponding point on the screen. In practice, some diffusion should be expected, which would be caused by the experimental variations, e.g., the source cannot be made to radiate strictly along the straight lines; radiation can be collimated only in a narrow beam.
As discussed in “Perceptions of physical reality: Classical Theories – Forces,” up to about 1800, Newton’s corpuscular theory of light that considered the light to be made of tiny particles was widely accepted, although there were some observations at variance with it from the beginning, which were accommodated by some adjustments. In 1801, Thomas Young observed light in a double slit experiment, i.e., with S being a source of monochromatic light. What he observed was a central band of high intensity on the screen flanked by several bands of high intensity. In between each pair of high density regions, the intensity varied from high to very low to high again. This resembles the pattern produced by two interfering waves as shown in Figure 3 below, not by the particles as illustrated in Figure 2.

Figure 3. Interference pattern produced by a wave in the double slit experiment
(Image courtesy Wikipedia.org)
An interpretation of the observation was obvious: S produces a wave, which is divided in two identical wavelets by the slits that interfere with each other to produce an interference pattern on the observation screen with C, D, E and F being the high intensity regions formed by the crests falling on crests and troughs, on troughs. From this observation, Young concluded that light was a waveform, which was confirmed by later experiments. Almost straight line followed by a light ray in a macroscopic observation was shown to be the result of the wavelength being small, which implies that the deviation from a straight line are quite small; finer measurements like Young’s were needed to show the pertaining details. Maxwell’s formulation and the observations of Hertz confirmed that light was an electromagnetic wave. This view persisted as “final” until Planck’s formulation assigning also the particle characteristics to light as described above.
Around 1925, Davisson and Germer were studying the surface properties of nickel by scattering the electrons from it. During the experiment, some air entered the chamber by accident, producing an oxide film on the surface. To remove the oxide layer, they heated the specimen to a high temperature. This produced a polycrystalline structure on the surface in the form of a diffraction grating, which they did not realize. Continuing the experiment, they collected the data, which showed unexpected diffraction-like pattern. A diffraction pattern is produced by the interference of wavelets and thus, it is essentially a double slit phenomenon. Davisson and Germer published the results without knowing their significance, which were used by Max Born in a conference, attended by Davisson, to support de Broglie’s hypothesis that the material particles possess wave-like characteristics. Then further experiments were conducted concluding that the electrons are also waveforms as Young did in case of the photons. On the other hand, electrons were understood to be “definitely” particles from the previous observations in a variety of experiments. So were the photons, as discussed above. Finer measurements in the double slit experiment also reveal their particle behavior together with the wave nature, which will be discussed later. For now, we introduce the material as it developed initially.
Wave-Particle Duality
A very puzzling situation had developed: Material bodies we thought were particles are also waves and the structures that we thought were waveforms are also particles. The puzzlement was for the reason that the two entities as we understood them classically are mutually exclusive. To clarify, their main distinguishing characteristics are described below:
Free particles are localized in space and time and isolated from each other as verified by a variety of phenomena, e.g., a particle detector with a small aperture registers each single entity and does so almost instantaneously. In contrast, the waves are globally connected disturbances in the fields affecting wide regions transmitting energy in a continuous manner.
Particle-density reaching a region in space from different places by different routes are added together to produce the resultant density; one plus one is always equal to two. The amplitude of the resultant of two overlapping identical waves is obtained by superposition, i.e., by adding the amplitudes where one plus one can be equal to two, zero or anything in between depending on the phase-difference between the two waves. In addition, the intensity of a wave is the square of absolute value of the amplitude making the intensity a more complicated quantity than the particle density, which is to particles what the intensity is to a wave.
To reconcile these two attributes, the doctrine of wave-particle duality was forged: Each of these physical entities is a particle as well as a wave; i.e., the terms “Particle” and “Wave” represent the same physical entity, same physical reality; each entity has a dual character, particle and wave; both characteristics exist together. The terms “particle” and “wave” are still used in the classical sense for convenience and clarity of descriptions. The fact that a particle is a localized entity was accommodated in the waveform by arguing as follows: Many waves superposed on each other can interfere to produce a wave with large amplitude with a central peak tapering off as the distance from the peak is increased; a particle, quantum, is essentially the envelop of the resultant wave, called the “wave packet.”
Rationalizations were developed to “reconcile” the dual nature of these entities. It was argued that they are like an elephant observed by seven blind men each one describing it with a different attribute depending on which part one touched: One who touched a leg thought it was like a tree; one who happened to touch its trunk, thought it was like a python; one who grabbed its tail thought it was like a rope; ... while an elephant is all of these put together. Similarly, these entities are waves as well as particles; each attribute is observed depending on the experiment. Their duel nature was also rationalized by suggesting that they are emitted and absorbed as particles but travel as waves. They were also thought to be particles individually but waves in a collection, individuals interfering with each other. Another thought was that they have no form until observed, i.e., the observation determines the form of each entity assigning a crucial role to the “observer” in defining the physical reality.
If unsettled by this state of affairs, a reader can take solace in the fact that one is not alone; the reader is in the company of many from the practicing physicists to the philosophers of physics starting with the pioneers of the theory, to the present. Each one of the rationalizing arguments remained unconvincing and the issues related to the wave-particle duality still plague the quantum theories, which will be discussed. It may be remarked however, that our understanding of the situation has improved with subsequent work over a period of time, which still continues. For now we describe briefly, the formulation developed based on the doctrine of the wave-particle duality.
It should be pointed out that all the concepts of the quantum theories apply to all physical systems, e.g., to Moon as much as to an electron and a photon. It is just that the consequent effects are noticeable in case of the microscopic entities; for large systems, the effects are too miniscule to be of any practical consequence or even detectable as they get overpowered by other relevant large quantities. Nevertheless, these concepts and the formulation describe all systems, in principle.
Formulation of Quantum Mechanics
In this section, we outline the basic principles underlying the formulation of quantum mechanics in response to the dual nature of the physical entities under consideration.
Since a particle is a wave, definition of its state in terms of the classical particle attributes, e.g., the momentum and position; were rendered inadequate. Taking a clue from the classical theory of waves, a mathematical function of global extension, called the wavefunction, was considered to provide an adequate representation of its state. Since the state is a wavefunction, a wave equation was searched for describing its evolution. Schrödinger, using heuristic methods and intuitive reasoning, developed his equation, which yielded correct spectrum of the hydrogen-like ions. The solution of this equation provides the state function or wavefunction of a physical system, which is the electron in the orbit in the present context. The superposition principle applicable to the waves was adopted for the particles, which states that if two states are possible for a system, their linear combination is also a possible state. Dirac is known to explain the superposition principle to his students as follows: He would break the chalk in his hand in two pieces and place each at different spots on the table. Then he would explain that classically, a particle can be only at one of the spots; quantum mechanically, it can be at both spots and everywhere in between without having a diffused structure, i.e., maintaining its localized character. It should be mentioned that this is a very limited expression of the superposition principle but illustrates the point.
Born accommodated the particle nature by assigning the probability of finding the particle in a region of space calculated from the wave-function, known as Born’s rule. Thus, it cannot be said where a particle is; all one can do is to determine the probability of a particle being in a region about a point. In Dirac’s example, the particle is localized but the probability distribution defining its location is diffused.
Physical observables such as the position and momentum of a particle were then represented by mathematical operations. Physical values of the observables were assigned their expectation values calculated in terms of the operations representing them and the wavefunction. Classically, the observables such as the position and momentum are defined with certainty having definite values; quantum mechanically, they have a spread: In general, each measurement of a physical attribute yields a definite value but not the same; different “identical” measurements would yield different values spread over a region after many measurements. The expected value provides a type of aggregate of all values. This state of affairs was accommodated by assuming that each single measurement of an observable in a state, which may be a linear combination of infinitely many states, yields a “proper value” for the observable, with a probability assigned to each outcome.
As a consequence of the quantum mechanical formulation as described above, it was found that certain pairs of physical observables, e.g., the position and momentum of a particle, cannot be determined exactly simultaneously. An exact determination of one renders the other completely undetermined. In a simultaneous measurement of such pairs of observables, there is a positive lower limit to their accuracy. This is known as Heisenberg’s uncertainty principle. This limitation is not a result of the measurements; it is an inherent characteristic of quantum mechanics, i.e., quantum mechanically the values of such observables cannot be described simultaneously with certainty, even in principle. This is in a sharp contrast with the classical understanding.
As indicated above, outcome of a measurement is not definite; there are infinitely many likely outcomes, each one with a probability and there is an uncertainty associated with the determinations. This state of affairs, together with others, was unsettling to many. Einstein, in spite of having made some meaningful contributions to the quantum theory initially, was its strongest opponent. He is known to have argued: “Subtle is the Lord, but not malicious. God does not play dice with the World.” Niels Bohr countered, “It is not up to the scientists to tell God how to run his Universe.” Hawking added to the discussion much later, “God not only plays dice with the Universe, He also hides it in places where no one can find it.” Supporters of quantum theory are as disturbed as opponents by its founding structure. Bohr, in spite of having been among its staunchest supporters, has commented, “One who is not shocked by quantum mechanics, does not understand it.” Schrödinger in spite of having developed the most pervading equation in quantum mechanics had commented that he regretted to have had anything to do with quantum mechanics….. In spite of all that, rules of quantum mechanics have been immensely successful in predicting the outcomes of experiments. Major advances in science and technology, from the development of the nuclear reactors to semiconductor chips, are results of the quantum mechanical formulation and methods. The phrase “Shut up and calculate” is often used by the established physicists to respond to the inquiring budding minds, indicating this state of affairs. Those who question the fundamental structure of quantum mechanics are “shut up” by citing its successes. Einstein himself has been compared with a “dog who barks every time the truck of quantum mechanics passes by but he can do nothing about it.” However, human inquisitive urge cannot be suppressed; various efforts to disentangle the mysteries continued and continue still. These matters will be taken up in the following articles in this series.
04-May-2014
More by : Dr. Raj Vatsya

|
If this article presents classical science as a system of clarity and that of quantum science as a bewildering one, it is nevertheless the case that science has been flawed from the outset in the absolute definition of what is observed. Thus an atom or an electron are actually abstractions of identity that science determines as the reality it observes. The phenomenon of identity, an absolute term, is the basis of, yet nowhere is explained by science as to first principles, on which is built its entire edifice. Put simply: what is identity? - identity by which any form is defined in absolute terms. In identity terms, things prove to be conceptual in nature - since they are retained as concepts, atom or electron etc.. The cunning of science is to call this 'observation' of the material particle so named. In fact, whatever science observes in absolute terms does not exist except as a contextually realised percept that has affective qualities as pertaining to its contextual identity. This same principle of ‘observation’ applies at the quantum level of particles: it is always a case of an absolute defining of something retained as a concept, proving that conceptual realisation is the basis of realisation of the quantum event. The context defines the identity that it realises. It follows that what emerges in the macro world of classical concepts of reality as contextual identity form realisation emerges in the micro world of quantum events in like manner, and that the power determining form is a contextual one, whose affective power is endowed on each realised form. |

|
A very stimulating article with remarkable clarity on such a diffused state of what we call reality. I loved your quote about Einstein barking at the quantum mechanics truck every time it passes by. Your other mention of the phrase "shut up and calculate" is also very intriguing. We clutch on mathematics when the visualization is rendered helpless. |