In our schools and colleges teachers will monotonously give a routine of exercises to the students. There will be many numerical examples but at no point of time, they try to understand the correlation between their algebraic formulae and the numerical examples.

Let me explain with some concrete examples.

You ask any teacher, whether he teaches degree or high school classes, or any student, what is (a + b) multiplied by (a - b)? [Or, to put it in notation what is [(a + b) x (a – b)]

No doubt, they will promptly answer (a² – b²)

They are right.

Then ask them, in an arithmetic progression with common difference d, in a set of 3 consecutive terms, what is the relation of the middle term with the other two?

They will definitely say middle term is half of their sum.

Then, you ask them for fun, in a set of 3 consecutive natural numbers, you got the product of the 1st and 3rd term as 7743. Then what is the square of the middle number. Mind you, you did not ask what that middle number is. Only asked what is its square?

I am pretty certain most of the people will take more than 5 seconds to answer.

If they take more than 5 seconds, (because I suppose it takes that time to sink into the mind the verbal expression), you tell them that you want to ask another question.

Again, in a set of 3 consecutive natural numbers, sum of the 1st and 3rd numbers is 100. Then what is the square of the middle number?

Incidentally, you also ask them how they arrived at the answer.

I am sure most of the students and teachers do an elaborate set of calculations. If they are intelligent, they take the sequence of numbers as (a-1), a, (a+1) (because the set of natural numbers is an arithmetic progression with first term 1 and common difference 1). Otherwise, they follow their own method to arrive at the answer.

Let me explain the disconnect I am talking about in detail with reference to the two questions mentioned above.

Teachers and students are very good in explaining or doing the sums relating to algebra or other subjects. But, what they lack is the ability to see the inter relation between the formula and problem at hand.

In the first question, I asked the square of the middle number, giving the product of the two neighboring numbers.

Literally, I gave them the product of (a-1) and (a+1)

In a sequence of 3 natural numbers (a-1), a, (a+1), I gave the product as 7743. Naturally, the square of the middle number is got by just adding 1 to it. The answer is 7744. How much time will it take to add 1 to the given no? How much time is fair?

The point I want to say is, teachers won’t tell the students that the square of any natural number is got by just multiplying the two numbers to its right and left and then adding 1 to it. To put it the other way, the product of the two neighbouring numbers is 1 short of its square.

Thus,

Square of 15 is    14x16 +1

Square of 99 is    98x100 +1

Teachers and students will say (a+1)² = a²+ 2a+1 = [a²+ a + (a+1)]

They don’t see in it the third expression or the following interpretation:

‘(a+1)²’ is simply the square of any number (a+1) which will be to the right of ‘a’ in a set of natural numbers.

The expression in bold means, to get the square of any number (a+1), just add to the square of the preceding number (a²), the sum of the preceding number and the given number [(a) + (a+1)]

In practical terms, when you know the square of 16, just add 16+17= 33 to it.

That is, given 162 = 256;

Then, 17² = 256 + 33= 389;

18² = 389 + 17+18 = 424;

19² = 424 +18 +19 = 461;

And 20² = 461 + 19 +20 = 461 + 39= 400. And so on.

(There are several ways to get a solution. My contention is, to get a solution is different from the ability to see a larger relation amongst the subjects).

Similarly, for the second question I said:

We know, (a+1) + (a - 1) = 2a.

Therefore, a²is nothing but the square of its half.

If this intrinsic relation between numbers is known, when I gave them the sum of the two neighbouring numbers of the arithmetic progression as 100, the square of the middle number is simply 50² or simply 2500)

There are several ways to get the square of a number.

1. Square it directly. Useful only when the number is small.

2. Add ‘Unity’ (one) to the product of numbers on either side of it

3. Multiply the ‘sum’ of the immediate two numbers on either side by half of the given number; or, halve the ‘sum’ and then square it.

4. Taking any arbitrary nearest 10 multiple to the given no. and using (a + d). (a - d) = (a² - d²), adding / subtracting 1, 4, 9 or 16 to the product. (For any given no. ‘a’ (which is not a multiple of 5), we can see that either (a + d) or (a - d) where d= 1,2,3 or 4, is a multiple of 10. Using (a + d). (a - d) = (a² – d²), by adding d² to the product we can get a². Taking 10 multiple is to easily find the product.

5. As a corollary to 4, the square of any 5 multiple, which can be written as (10x +5), one need to work out from hundreds’ place and above only, since, the numbers in ten’s and unit’s place are always 2 and 5. [(10x +5) can be written as x5 if the place of x indicates place value 10, and place value of 5 is units. Similarly, 100x can be written as x00 where the place value of x is 100’s. We know (10x + 5)² = 100x² + 100x +25 which can be written as 100x(x+1) +25. As per the above notation mentioned, this means, x(x+1) will be in 100’s place and tens and units are always occupied by 2 and 5 respectively.]

And there are many others one can innovate.

However, in a world of rat race, there is no room for exploration or innovation. A text book solution has got to be reproduced.

In an excellent article how the teachers should identify and nurture gifted students, (which is a tall order in the present conditions of cut-throat competition), Mr. PK Srinivasan (The Mathematics Teacher Vol. 61, No. 4 (APRIL 1968), pp. 396-398 (3 pages)) gives an interesting account from the life of the great Indian mathematician Ramanujan. This shows to what great heights a child properly encouraged at the right time can raise to.

The context of the discussion was how an intelligent child gets bored of monotony and finds innovative ways to get off the boredom. And in those exercises he gives vent to his creativity. The teacher has to spot and nurture that talent. Coming to the point, Mr. PK says,

“Any 9th grade teacher or student can say:

(n+2)² is n² + 4n + 4

And similarly, can factorize

(n² + 4n +3) as (n+3). (n +1)

But can you imagine a 9^th grader attempting to prove

?

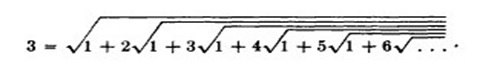Ramanujan has written

(n+2)² = 1+ (n+1). (n + 3)

And taking square-root on either side, he obtained

(n+2) = Sq. root of [1+ (n+1). (n+3)]

Unless the child has an aesthetic sense, he cannot notice that it is a relation between 3 consecutive numbers. (As described in above examples)

He, went on further to explore.

Multiplying both sides by n, he got

n. (n+2) = n √ [1+ (n+1). (n +3)]

This is a beautiful property between 4 consecutive numbers.

He went on further.

He defined [f(n)] = n. (n+2)

And

f(n+1) = (n+1) .(n+3);

Now you can see the magic:

Don’t be harsh on your child when he/ she wants to experiment something however absurd it might seem to you. Try to encourage the child to be innovative. Don’t nip the urge to be original in the bud.

References:
1. The anecdote on Ramanujan Courtesy:
https://www.jstor.org/stable/27957856?read-now=1&loggedin=true&seq=1#page_scan_tab_contents"