Dec 20, 2025
Dec 20, 2025
by C. K. Raju
Don’t cancel the calculus, make it easy!
Abstract
Regardless of whether the axiomatic method is found in the “Euclid” book, are axiomatic proofs “superior”? The inferiority of deductive proof was asserted by the Indian Lokayata, and its high fallibility has already been explained in an earlier article. We now explain how axiomatic proofs make even 1+1=2 enormously difficult without adding an iota of practical value. This is also true of the calculus: on the axiomatic method, real numbers are deemed theoretically necessary for calculus, but never used in any practical applications to science and technology. But is there epistemological clarity in calculus without real numbers and limits? Yes. The Indian calculus originated with a different epistemology, using non-Archimedean arithmetic instead of real numbers, hence there are infinities and infinitesimals, hence no limits. Instead, zeroism was used to sum infinite series, as first summed in India. The axiomatic method, of using “reasoning minus facts”, actually originates from the politics of the Crusading church theology of reason, but was brazenly imputed to Greeks by “reinterpreting” the “Euclid” book, when it first arrived in Europe as a Crusading trophy. Globalisation of colonial/church education spread this inferior way of doing mathematics throughout the world. Axiomatic math only provides a worthless metaphysical coating over normal math, which provides all practical value. However, the difficulty of axiomatic math has made the vast majority ignorant of math, and colonial education taught them to trust only Western mathematicians, who have a vested interest in it, and refuse to publicly debate it. This combination of ignorance and misplaced trust is a recipe for perpetual mental slavery. While this propaganda succeeded, it now spells disaster for the US in the technology race.
Are axiomatic proofs superior?
To summarise part 1 of this article, the new California math framework “cancels the calculus” because of the difficulties in teaching and understanding the calculus. These difficulties only reflect the historical European failure to understand the calculus. Those difficulties arose because calculus was stolen from India, and knowledge thieves often fail to fully understand what they steal. The later-day epistemology of real numbers, which the West added on to the calculus, is too difficult to teach at the K-12 or beginning undergraduate level. As such, a simple alternative is to revert to the original Indian epistemology of the calculus. However, the Western pretensions, of having invented a “superior” way to do mathematics, stand in the way of accepting an alternative epistemology. Those pretensions are tied to a whole lot of false myths surrounding “Euclid” and “Pythagoras”.
According to those false myths the “Euclid” book has axiomatic proofs. But, regardless of whether “Euclid” existed, and regardless of whether the color of his skin was white, as Wikipedia and Indian school texts misleadingly suggest by showing children fake white-skinned images of “Euclid”, the fact is there are no axiomatic proofs in the “Euclid” book. The actual proof of the “Pythagorean” theorem in the “Euclid” book does NOT use any different principles from its Indian proof, hence is NOT in any way superior. Only the myth about the proof says it is different.
As this part now explains, axiomatic proof historically originated not from any Greeks but from the politics of the Crusading church, and its theology of reason.
To begin with, regardless of its historical origins, one can nevertheless ask the purely philosophical question: are axiomatic proofs superior?
The stock answer given by mathematicians today is that empirical proofs are fallible, while axiomatic proofs purportedly are infallible. That too is complete balderdash: as I have explained in detail,[1] axiomatic proofs are not only highly fallible, they are more frequently fallible than empirical proofs: because the mind errs more easily than the senses. The claim that axiomatic proof has some superior epistemic value is completely false.
Since the above article is freely available online, I will not repeat those arguments here. Some simple arguments are obvious even to the layperson. As is well known, science relies on the empirical, i.e., it uses the experimental method, well recognizing its fallibility, as in the acknowledgement of experimental errors. Therefore, if one does mathematics for the sake of its applications to science and technology, admitting empirical methods of proof also in mathematics, as is done in Indian ganita, cannot do any epistemic harm. This argument is particularly relevant in the context of the Californian proposals for a changed math framework, which are geared to the anticipated needs of future technology, and especially data science, which is empirical.
The only Western response, so far, to my detailed arguments against the axiomatic method, has been to strike a superior pose and ignore me (as an “inferior” coloured person and non-Christian non-Westerner). Or they use propagandist monkey tricks, as in the racist South African press,[2] to try to vilify and grossly misrepresent me. The use of propagandist tricks (see above article for details) shows they want to oppose me, but the failure to engage intellectually corroborates that Westerners are far too afraid to engage publicly with even my philosophical critique of axiomatic math. Why? Presumably because the smarter one’s well know that my arguments are sound, difficult to contest, and my critique directly threatens the means of livelihood of all present-day university mathematicians, because colonial education globalised Western ethno-mathematics. Anyway, since my critique stands intellectually unopposed for two decades,[3] it should be deemed as accepted, and I will proceed accordingly.
So, here I will only spell out the practical implications of that critique, for the case of 1+1=2. We all learnt 1+1=2 in kindergarten. We were shown pictures of 1 orange and 1 orange making 2 oranges. However, this involves the empirical: for one must be able to see those oranges. And, recall what the current NCERT class IX text[4] sates: “Beware of being deceived by what you see...!" [Appendix 1, p. 301].
So, what is the supposedly right way to do things? As the same text says, in the same place: “each statement in the proof has to be established using only logic....” (emphasis original). Bertrand Russell, though he was well aware that the claim of axiomatic proofs in the “Euclid” book was 100% false, nevertheless accepted the philosophical belief that there is something “superior” about axiomatic proofs. In his magnum opus, the Principia,[5] he provided such an axiomatic proof of 1+1=2, which took him all of 378 pages. Most people never read those 378 pages, and are unlikely to understand even a single sentence on that page 378.
The important point here is that the claim of “superiority” certainly does NOT mean superior practical value. People were using 1+1=2 for thousands of years before Russell, and continue to do so today without the slightest knowledge or understanding of what Russell did. Indeed, in a grocer’s shop, one has no choice but to use the empirical, and Russell’s axiomatic proof of 1+1=2 is a positive impediment, because of its extreme prolixity and difficulty.

That is, the axiomatic method adds immensely to the difficulty of mathematics, but nothing to its practical value. The axiomatic method creates a chasm between the theoretical understanding and the practical usage of mathematics: most people manage to do complex practical tasks without that theoretical (axiomatic) understanding
The use of the axiomatic method is the reason why colonial education (which globalised Western ethno-mathematics) made math so difficult to learn. That is, the subject has been made difficult, it is NOT the students or teachers who are fault for the notorious difficulties of math.
Let us now apply this to the case of the calculus.
Real numbers
Recall that the Californian proposal to “cancel the calculus” is based on the observation that students doing the calculus at the K-12 level fail to understand it. Recall, further, that this difficulty arises because the notions of real numbers and limits are basic to the definitions of derivative and integral, at the core of the calculus. The difficulty of real numbers and limits is clear from the fact that these notions are left undefined in school texts and the fat “Thomas’ Calculus” texts, as we saw in Part 1 of this article.
Recall, finally, (as also explained in Part 1) that Dedekind invented real numbers in order to avoid the empirical observation used in the proof of the very first proposition in “Euclid’s” Elements. That is, real numbers were invented to enable an “axiomatic” proof of that first proposition, to “save the myth” of “superior” axiomatic proofs in the book. Dedekind’s definition used Cantor’s set theory which was later rejected as confused, and full of paradoxes such as Russell’s paradox.[6] The precise (axiomatic) definition of “real numbers” requires (at least[7]) axiomatic set theory, which developed only in the 1930’s and is so hard that it is studied by few even among professional mathematicians.[8] This makes it very hard to understand or prove even 1+1=2 in real numbers.
Note that in axiomatic mathematics, 1 as a natural number is a different entity from 1 as an integer or 1 as a rational number, or 1 as a real number. The need for axiomatic set theory in defining 1 as a real number makes it much harder to prove 1+1=2 in real numbers than Bertrand Russell’s 378 page proof of 1+1=2 in cardinals. Thus, after a panel discussion in the University of Cape Town,[9] I asked the participating (senior) mathematician if he could even prove 1+1=2, and he wrongly replied that one should use Peano’s axioms. When I pointed out that my challenge related to the real number 1, to which Peano’s axioms did NOT apply, he had no serious response.
This “Cape Town challenge” publicly demonstrates the difficulty, even with 1+1=2, in axiomatic real numbers. The challenge is to (axiomatically) prove 1+1=2 from first principles, which challenge was repeated in JNU with a prize of Rs 10 lakhs, for the proof provided overnight, and a reduced prize of Rs 1 lakh for the proof provided within a week.[10] Admittedly, JNU is mostly for social science, and social scientists are often bad at math. But, after all, even social scientists need statistics, which needs calculus and real numbers. Hence, real numbers are taught as part of compulsory math in class IX (chp. 1 in the class IX NCERT text), so that anyone, student or faculty, in any university ought to know about them. Of course, as anyone would have guessed by now, the class IX text does NOT actually define real numbers: students are just expected to nod in class, and pass an exam, which avoids such difficult questions as the proof of 1+1=2.
To summarise, the difficulty of understanding the calculus is due to limits and real numbers. These difficulties are primarily due to the axiomatic method in mathematics which makes the calculus (and real numbers) hard to understand without adding any practical value, just as Russell’s axiomatic proof of 1+1=2 is hard to understand but does not add an iota to its practical value.
Floating point numbers
To be quite precise, by “practical value” I refer to common practical applications of the calculus to science and technology (such as calculation of rocket trajectories). These today involve the numerical solution of differential equations on a computer. Further, though real numbers are deemed essential to the calculus as taught in schools and universities, a computer cannot use formal real numbers (because they are actually unreal or metaphysical).
Instead, a computer uses floating point numbers.[11] But floating-point numbers have a completely different algebraic structure: for example, the associative “law” for addition, which holds for real numbers, fails with floating point numbers,[12]
![]()
In short, all practical applications of the calculus (to science and technology) can be and are achieved without using real numbers, the primary stumbling block in the teaching of calculus.
Political value for the church
There is, however, a caveat: the huge difficulty of axiomatic mathematics makes the vast mass of colonially educated people ignorant and frightened of mathematics, and colonial education teaches them to blindly trust Western opinion in the matter, and refrain from forming their own opinion. That is, this axiomatic mathematics, globalised by colonialism, has great political value for the colonizer. That is, colonial math has a political use in ensuring Western/colonial dominance.
There are other political uses: axiomatic math actually arose, not due to any Greeks, as Crusading myths of “Euclid” etc. claim, but as a political requirement of the Crusading church and its rational theology. It still remains of major political value to the church, enabling the church to smuggle in its metaphysics into science[13] in ways which are beyond the comprehension of most people. We will return to these issues later.
“It works”
This critique also raises a common doubt. “It works” people say of present-day mathematics. The simple answer to this is as follows. Normal math (or ganita, which accepts empirical proofs) works and has worked for thousands of years. The axiomatic method was an add on to this: for example, Russell’s axiomatic proof of 1+1=2 came in the 20th century, though knowledge of 1+1=2 existed for thousands of years before that. As we saw, the axiomatic method added nil practical value.
Hence, while 1+1=2 “works”, it is excessively foolish to give credit for that to axiomatic mathematics which was simply a later-day add-on, which added absolutely nothing to make 1+1=2 work better in a practical context. Likewise, the calculus existed for centuries before axiomatic real numbers (even on the false myth that Newton and Leibniz invented the calculus). And we just saw that real numbers add nothing to the practical value of the calculus, which is today obtained using computers which cannot use real numbers, but use floating point numbers instead.
The decolonised (Indian) calculus
This extensive background makes it easy to understand why Indian ganita makes calculus easy, without diminishing its practical value. Obviously, the first step is to get rid of the axiomatic method, based on silly and false myths of Euclid and Pythagoras, which only adds to racist and Western boasts of superiority. The following are the details.
The actual Indian invention of calculus was geared to its practical use. Indeed, the first practical use of the calculus in India was by the 5th c. Aryabhata who derived precise trigonometric values (precise to the first sexagesimal minute or about 5 decimal places),[14] for their use in astronomy (hence celestial navigation). For this, Aryabhata used a numerical (finite-difference) technique today falsely[15] called the Euler method of numerically solving differential equations.
This understanding of calculus as concerned with the numerical solution of ordinary differential equations is central to the teaching of decolonised calculus. Note that this bypasses both the difficult notions of derivative and integral as some sort of “limits”. Only finite differences are needed at any time, hence no notion of derivative is needed.
People also wonder where is the integral sign? Obviously nowhere. But, numerically solving an ordinary differential equation is itself a more general process than integration, regarded as the anti-derivative. Therefore, the integral sign was never needed or used in India.
Related notions of functions, such as the exponential function, or the sine and cosine functions, are now defined not by using triangles etc., or even infinite series, but primarily as solutions of ordinary differential equations. As such, the values of these functions are easily calculated and visualised, as is done e.g. by my software CALCODE.[16] The method of summing infinite series comes later.
It is this which makes the decolonised calculus easy while enabling students to solve much harder problems.
Aryabhata’s numerical method (“Euler’s” method) involved a technique of linear interpolation/extrapolation (“rule of three”, or trairashik) which, though widely applicable and easy to understand, is not numerically the most efficient. Hence, this was soon (about a century after Aryabhata) criticised by Brahmagupta (7th c.) who extended it to quadratic interpolation. Eventually, it was extended to higher order (11th/12th order) methods of interpolation/extrapolation by Aryabhata’s followers in Kerala.[17]
This is good enough for all practical applications of the calculus (such as calculation of rocket trajectories) which today involve numerical solution of differential equations on a computer.
Hence, also, my alternative way of teaching calculus (“5-day course in calculus”) emphasizes that calculus is basically about the approximate numerical solution of differential equations. This preserves the practical value that one expects to derive from calculus, and makes it easy.
Alternative epistemology 1: non-“Archimedean” arithmetic
But what about epistemology? What about understanding? The critical difference again is that the calculus in India developed without real numbers, and without the use of limits, all of which came to Europe long after the supposed discovery of the calculus by Newton and Leibniz.
The critical difference (in terms of axiomatic math) here is that real numbers are characterized as the largest system of numbers (technically the largest ordered field) with the so-called Archimedean property. The Archimedean property (nothing to do with Archimedes) says that any positive real number is less than n for some integer n.
This actually concerns algebra. The word algebra derives from the text al jabr wa’al Muqabla of al Khwarizmi, of the Baghdad House of Wisdom, which focused on linear and quadratic equations. Al Khwarizmi, however, only translated a part of the earlier work of the 7th c. Indian mathematician Brahmagupta.[18] The latter, of course, solved linear and quadratic equations, but he also did the arithmetic of polynomials, which he called “unexpressed” arithmetic (avyakt ganita).[19] That is, he treated polynomials such as 2x+3 as “unexpressed” numbers, which behaved algebraically almost like ordinary numbers, but acquired a numerical value only after the numerical value of x was specified.
In present-day terminology, polynomials (with “rational” coefficients) constitute an integral domain: there are no zero divisors. If the product of two polynomials is zero, one of them must be zero. This means that one can also divide one polynomial by another the way one divides one integer by another. Hence, one can also have polynomial fractions, or a ratio of two polynomials (today called rational functions).
A special feature of the arithmetic of polynomial fractions (or rational functions), as compared to the arithmetic of integer fractions, or ordinary arithmetic, is that with polynomial arithmetic, the so-called “Archimedean” property (AP) fails.[20] (To reiterate, this terminology is historically inaccurate and racist, Archimedes had nothing to do with it.) The AP says that any positive number can be made less than 1 added to itself n times. The failure of AP is quite obvious because the polynomial x may be larger than n whatever the preassigned n one may choose. That is polynomial arithmetic is what is today called non-Archimedean, whereas ordinary integer arithmetic or the arithmetic of real numbers is Archimedean.
In the context of calculus teaching, the special features of non-Archimedean arithmetic are that (a) it involves infinities and infinitesimals, therefore (b) (unique) limits do NOT exist (therefore, one does NOT have to worry about “completeness”). This non-Archimedean arithmetic first came into the limelight among Western mathematicians in the late 1960s, in the context of Robinson’s Nonstandard analysis. Then it was pointed out that the rigorous use of infinities and infinitesimals was possible and even permitted a more intuitive understanding of the calculus. In the case of Nonstandard analysis, the claim of a more “intuitive understanding” is deceptive, because learning nonstandard analysis itself is not very intuitive. Hence, it was not pursued.
However, in the case of Brahmagupta’s polynomial arithmetic there is no such difficulty. All it involves is school algebra. In nonstandard analysis, the infinities and infinitesimals are required to appear only at an intermediate stage, not in the final result. With polynomial arithmetic, they do not go away: they are permanent so to say. Because of the presence of infinitesimals, exact limits do not exist with non-Archimedean arithmetic. For example, one can no longer say that the limit of 1/n is 0; but only that when n is infinitely large 1/n is infinitesimal.
However, infinite sums can be understood without the use of metaphysically exact limits. Thus, the fact remains that the 15-16th c. Indian mathematician and astronomer Nilakantha did correctly state the sum of the infinite geometric series.[21] He was the first to do so. The sum of an infinite series is something that is regarded today as correctly doable only with the use of limits or real number or the continuum: so how did he do it? As I have explained,[22] this involved just the simple formula for the sum of a finite geometric series, together with the neglect of infinitesimals.
Alternative epistemology 2: Zeroism vs exactitude
That brings us to a third fundamental difference between the Western understanding of mathematics, and the Indian understanding of mathematics, called ganita. Westerners believe mathematics is an exact science. This, of course, is just another piece of bunkum. For example, where in the world is the “Pythagorean” theorem exactly true? Obviously not on the curved surface of the earth, as the Indian mathematician Bhaskara 1 asserted[23] in the 7th c., long before “non-Euclidean” geometry. Obviously, also, not in curved space time. At this stage Western apologists start jumping to say that it is approximately true. However, the immediate question is about exactitude, which clearly fails in the real world. Moreover, there is simply no concept of “approximate truth” in axiomatic mathematics which is all about the true-false binary. Even the NCERT class IX text (Appendix 1, sec. A1.6) states this: “In [axiomatic] mathematics, a statement is only acceptable if it is either always true or always false.” Moreover, an “approximation” is worthless unless the error is specified, which is never done for the “Pythagorean” theorem.
In contrast, Indian ganita (like science) accepted approximate calculations from the earliest times. For example, the sulba sutra uses the term savishesa (meaning “with something remaining”), Aryabhata uses the term asanna (meaning “near value”), and specifies his precision (first sexagesimal minute) etc. Indeed, according to the Buddhist philosophy of sunyavada, and my related philosophy of practical zeroism,[24] the belief in exactitude is erroneous because nothing in the real word can remain exactly the same even for two instants. Of course, once again this inexactitude makes no difference to the practical applications of the calculus, which, as already stated, only involve inexact numerical solutions. The solutions, though inexact, may be precise for practical applications, as in the 14th c. Madhava’s value of π precise to 11 decimal places.
However, the belief in exactitude of mathematics is critical to the difficulties in teaching of the calculus. The purported need for real numbers, and limits (regarded as too difficult to be even included in the fat “Thomas calculus” texts), arises just because of the question: “what is meant by the EXACT sum of an infinite series?”. (Inexact sums of infinite series are used all the time, e.g., in the S-matrix expansion of quantum field theory.)
Neither Newton nor Leibniz could explain how to sum an infinite series EXACTLY, something which Descartes thought was beyond the human mind. Alluding to the infinite series for π [from India], or the ratio of a curved line (the circumference of the circle) to a straight line (its diameter), Descartes[25] declared this was something which was beyond the human mind, because he believed mathematics must be exact.
Descartes evidently also believed that to sum a series one must sum it term by term. But if one does that for an infinite series then in finite time one can sum only a finite number of terms. That means the sum of an infinite series often cannot be exact, because some terms are left out. But summing an infinite number of terms would take infinite time, especially if there is no pattern, as in the digits of π. So, an exact sum is impossible, in reality. The invention of real numbers and limits solved this problem – of understanding the meaning of the exact sum of an infinite series – for Europeans, but in a completely metaphysical and unrealistic way.
Four centuries earlier, Nilakantha had solved the same problem of summing an infinite series, in a far simpler way by, using non-Archimedean arithmetic and discarding infinitesimals. But the West never understood that to this day, and is unwilling to reject its related (religious) beliefs about exactitude in mathematics. To start with, Nilakantha used the simple formula for the sum of a finite geometric series. In terms of Brahmagupta’s polynomial fractions,
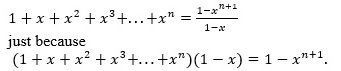
However, if x<1 then when n is infinitely large (remember we are using non-Archimedean arithmetic), then xn+1 is infinitesimal and can be discarded, without serious loss of precision. That gives the sum of an infinite series ![]()
The feasibility of this way of teaching calculus, the way it actually developed in India, has already been demonstrated in pedagogical experiments conducted in three countries, as already pointed out at the beginning of this article.
The religious roots of Western mathematics
So, does that mean that the world will adopt this method and start teaching calculus as it originated in India? That seems unlikely for some reasons that need to be widely known.
The first thing is that, while Indian ganita was always practical, Western mathematics has deep religious roots. The very word mathematics derives from the μαθησιζ (mathesis), as Proclus[26] explicitly informs us. The word mathesis notionally means “learning”, but Pythagoreans and Plato (Socrates) linked mathesis to soul arousal as Proclus also tells us:
"Pythagoreans recognized that everything we call learning is remembering…although evidence of such learning can come from many areas, it is especially from mathematics that they come....That is why Socrates in the Meno uses this kind of argument. [Questions a slave boy about geometry.] This part of the soul has its essence in mathematical ideas, and it has a prior knowledge of them…."
“Prior knowledge” refers to knowledge acquired by the soul in its previous lives, as Socrates clarifies in Plato’s Meno.[27]
"The soul, then, as being immortal, and having been born again many times, and having seen all things that exist, whether in this world or in the world below, has knowledge of them all; and it is no wonder that she should be able to call to remembrance all that she ever knew... for all enquiry and all learning is but recollection."
Proclus[28] explicitly derives the word “mathematics” from mathesis.
"This, then, is what learning [mathesis] is, recollection of the eternal ideas in the soul, and this is why the study that especially brings us the recollection of these ideas is called the science concerned with learning [mathematike]. Its name thus makes clear what sort of function this science performs."
This connection of mathematics to the (eternal) soul is the basis of the Western superstition that mathematics involves eternal truths, hence must be exact.
Incidentally, as I have pointed out[29] these ideas, linking mathematics to the soul, are not originally Greek but derived from Egyptian mystery geometry. But Egyptians also had a practical geometry, which used a rope similar to the Indian sulba, which Westerners set aside as “inferior”.
This mystery geometry is the reason for the apparent prolixity of the proofs in the “Euclid” book, from Alexandria in Egypt. The actual aim of the book is not the proof itself, but to put the reader in a meditative state, hence arouse the soul.
Mathematics and the Crusading theology of reason
The church first got involved with mathematics because of the linkages of (Western) mathematics to the soul. The “pagans” (Egyptians, Greeks etc. in the Roman empire) associated the soul with equity (hence Socrates picked a slave boy to demonstrate his beliefs about the soul). The Christian church, too, initially believed in equity (and in the very same notion of soul, similar to the Indian notion of atman). However, after the church married the state in the 4th c., it became highly political; it abandoned that notion of equity, and (indeed cursed[30] that notion of soul and shut down all schools of philosophy and mathematics in the Roman empire[31] by an edict in 531). The church ever since preached the “superiority” of Christians, often using secular arguments from false history such as Orosius’ shamefully false History Against the Pagans.
This methodology of concocting false history went viral during the Crusades against Muslims when the church appropriated all knowledge in Arabic books to Greeks. Euclid was a key aspect of this concocted Crusading history.
The significance of diagrams in “Euclid”
Indeed, a question which gullible Western scholars, under church hegemony, never asked is this: if Euclid really did exist, how come his ideas about geometry were so different from those prevailing among Greeks in his (purported) time, which ideas linked mathematics to soul arousal? Indeed, if one actually reads the “Euclid” book, the ideas in it are manifestly aligned to those “Greek” ideas of soul arousal through mathematics. For example, the book is full of diagrams, and diagrams relate to mathematics as mathesis. As Proclus explains (in the place cited above) while giving his etymology of mathematics:
"as Plato also remarks. ‘If you take a person to a diagram’ he says [Phaedo[32] 73b], ‘then you can show most clearly that learning is recollection.’ That is why Socrates in the Meno uses this kind of argument [i.e., draws a diagram to help the slave boy to recall his innate ideas of geometry].
Indeed, gullible Westerners did not find it surprising that “Euclid” so well anticipated a method of proof (reasoning minus facts) so politically convenient to the Crusading church that it adopted the book as a textbook. One can understand this, since Europe had a long Inquisitional tradition of brutally torturing and publicly burning suspected sceptics.
It was only the 20th c. that Russell could point out[33] that diagrams are irrelevant to axiomatic proof: “A valid proof retains its demonstrative force when no figure is drawn, but very many of Euclid's earlier proofs fail before this test”.
Indeed, recall again that the major difficulty of calculus teaching today is because of “real numbers” which were invented by Dedekind (about two decades before Russell’s above remark) just because the very first proposition of the “Euclid” book uses a proof involving a diagram.
So, how did Western scholars believe for so long (and still foolishly believe) that the “Euclid” book is about axiomatic proofs (though there are actually none in the book)? Because of church hegemony. Based on this manifestly false history (of axiomatic proofs in the “Euclid” book), and the related superstition that axiomatic proofs are “superior”, Western scholars hence adopted axiomatic proofs in mathematics.
Prohibiting facts benefits the church
The thing to understand is that axiomatic proofs—i.e., proofs which use reasoning but prohibit facts—were a key political requirement of the church during the Crusades. Thus, during the Crusades the church was forced to adopt reason. Whatever biased history church scholars may have written about the Crusades, they were, in reality, an attempt to convert Muslims by force the way pagan Europe was earlier converted by force to Christianity. But force failed against Muslims, forcing the church to resort to persuasion. But the church had no means of persuasion, for the Muslims also rejected the Bible as corrupted.
However, the Crusading spy Adelard of Bath, who was the first to bring the “Euclid” book to Europe, explained that Arabs accepted reason, as in the Islamic theology of reason. Therefore, the church too adopted reasoning during the Crusades, as the only way to persuade Muslims. This led to the creation of the Christian theology of reason of Aquinas and the schoolmen.
While the church accepted reason it could not also accept facts because numerous church dogmas, such as virgin birth, were contrary to facts. For example, when Aquinas proved his celebrated Aquinas theorem[34] that many angels can sit on a pin, he could hardly begin with facts for there are no facts about angels. Therefore, he just conveniently (“axiomatically”) assumed whatever he liked about angels, to prove his claim based on “universal” reason. And this is the sort of reasoning that our school texts sing paeans of praise about!
Indeed, reason + facts = science, and this is exactly what is used also in proofs in Indian ganita, but is contrary to the church use of reason. To meet its political requirements, the church praised the rejection of facts and observations as “superior”, and brazenly (and falsely) reinterpreted the “Euclid” book as an ancient book incorporating this church model of (metaphysical) reasoning without facts. As we have seen, the “Euclid” book is actually tied to the Greek understanding of geometry as mathesis, since Platonic times, and does NOT have a single axiomatic proof. But the church could hardly have accepted that Platonic understanding of geometry, as related to soul arousal, for it had long ago officially cursed the related notion of soul. But the church simply declared its model of (axiomatic) metaphysical reasoning as “superior”, and made its aim the aim of all mathematics. Actually, such math is inferior for purposes of (good) science and technology, but Westerners swallowed that claim of superiority (just as they swallowed the racist church claim that Whites are superior).
Such was the hegemony of the church over the European mind, that all Western scholars believed this church balderdash about “Euclid” for 750 years, and even today they continue believing it. Bertrand Russell who clearly understood the absence of axiomatic proofs in the “Euclid” myth, and was ostensibly against the church, also fell victim to this church propaganda about metaphysical mathematics as somehow “superior”. Westerners are not going to admit that, under church influence, the best of them made such complete asses of themselves for so long.
Will the West fall victim to its own propaganda?
However, with the help of colonialism and colonial education this sort of inferior mathematics has spread throughout the world, along with the related false myths (from Euclid and Pythagoras to the invention of calculus by Newton and Leibniz). That is because colonialism globalised the church system of education which prevailed in Europe until the 19th c. All the major Western universities, such as Paris,[35] Cambridge and Oxford were set up by the church during the Crusades. Indeed, Europe had nothing apart from church education: the first bill for secular education, only at the primary level, was introduced in Britain only in 1870.[36]
The false history of science[37] created by the Crusading church was used to assert Christian superiority, and this technique was later carried forward by racist and colonial historians to assert White/Western respectively.[38] This involved the same group of “superior”, human beings but only changed the labels used to describe them from “Christian” to White/Western. This false history of science was used to sell colonial/church education as “superior” to the colonised.[39]
It has certainly fooled the colonised who never realized the possibility that mathematics, as currently taught (not as it was earlier) may have a religious bias, and may no longer even be secular, as a subject taught compulsorily in schools ought to be. (Without going into the complex details, the axioms of present-day mathematics, set theory etc, all involve a metaphysics of infinity closely allied to church dogmas of eternity.[40]) This sort of math certainly ensured Western domination because, though the axioms are perfectly arbitrary, in principle, they are invariably laid down by Westerners, in practice. Mathematics is limited to furthering the Western fantasies about infinity/eternity.
Further, the resulting unnatural complexity of (actually easy) math arouses fear of math, which works exactly like the fear of god, used by the church to drive people into its arms. Thus, the first lesson of colonial education is to trust only “superior” Western or Western-approved sources. Therefore, the colonised people imagine that, because of their own ignorance of math, any decision in this matter can only be taken by university mathematicians, for whom the current system of axiomatic mathematics is a means of livelihood (as it once was for me). This is a recipe for perpetual mental slavery.
The black comedy in the above situation can perhaps best be brought out by an analogy. The ancient Indian Lokayata,[41] for thousands of years, criticised the Veda-s as just a means of livelihood for Brahmins. What if someone were to respond to this critique by saying that, since they know no Sanskrit or the Veda-s, the Brahmins are the one’s best suited to decide the truth of the matter? (I have answered that critique, but that is a separate issue.)
In India there were public debates, which ensure transparency. But the university mathematicians today avoid public debate, and assert that it is first necessary for any critique to pass through their system of secretive peer review, a system invented by the church as part of European academics, to preserve orthodoxy, for that is what secrecy does. Of course, every aspect of my above critique has been published in peer reviewed forums, but in some cases the referees were (presumably) not White or not Western which presumption makes it “inferior” according to the Western system of academic ranking,[42] hence no substantive arguments are needed! This is how implicit racist prejudices still decide truth in US academics.
However, while the West has admittedly been wildly successful in its propaganda, spreading it throughout the world, and mentally enslaving the colonised, the chickens have now come home to roost. The difficulty with the calculus shows the West has become a victim of its own propaganda. The Californian proposals show that the West now is trying to dumb down its math syllabus, as the only (bad) solution it has. However, despite colonial education, the non-West lacks a similar cultural attachment to Western myths and the related bad philosophy of mathematics: for the non-West has always valued mathematics solely for its practical value. Hence, it seems only a matter of time before that false Western history and related bad (church) philosophy of reasoning in mathematics is rejected.
Therefore, unless the West abandons the myths on which its false sense of “superiority” is based, and takes urgent corrective steps, it seems only a matter of time before it loses the technology race to others who are culturally more flexible.
24-Dec-2021
More by : C. K. Raju