Classical Theories - Geometrization

Present article is the 5th one in this series, which continues from the 4th: Perceptions of Physical Reality/ Classical Theories – Special Relativity cited here as [IV]; which together with the earlier articles cited there should be checked for explanations of some of the concepts appearing here. In [IV], I had discussed the history and concepts pertaining to the special theory of relativity covering electromagnetism and mechanics. It was natural to attempt to extend this formulation to include gravitation, which was the only other force field known at that time. Although some of the concepts developed are applicable to more general situations, formulation of the general theory of relativity focuses on gravitation.

As will be discussed, the general theory of relativity eliminates the concept of force from gravitation; instead, the theory describes gravitation in geometrical terms on the background of the Riemannian geometry; and thus, geometrizes gravitation describing it as a property of the spacetime. Hermann Weyl in his attempt to unify electromagnetism and gravitation developed his geometry. Although Weyl’s attempt remained unsuccessful, his concepts and geometry would have a profound impact later on various fields in physics. Kaluza, with some contributions later by Klein, attempted to develop an alternative to Weyl’s geometry by constructing a higher dimensional Riemannian space as the underlying geometry. However, the Weyl and Kaluza-Klein formulations ended up complementing each other. In any case, these formulations brought electromagnetism also in the realm of geometry. Describing the physical phenomena in terms of the properties of the underlying suitably constructed “spaces;” was a radical departure from the earlier ways, which were more mechanical. In the present article, I will discuss the concepts pertaining to the general theory of relativity as developed originally followed by the subsequent geometries and their impact on our understanding of nature and its workings.

Equivalence Principle

As was discussed in [III], (Note author’s correction in the comments) the gravitational mass of a body accelerated by the gravitational field created by another one is equal to its inertial mass. The gravitational mass of the first, accelerated body is called the “passive gravitational mass,” and the gravitational mass of the body producing the field is called the “active gravitational mass.” Recalling the example of a pebble falling to the earth, the gravitational mass of the pebble is passive and that of the Earth is active. If the focus is on the motion of the Earth in the field of some other body, which can also be the pebble, then the Earth’s gravitational mass is passive and that of the pebble is active. The labels “active” and “passive” serve mainly as the reference terms rather than having a substantial meaning. Also, strictly speaking, two bodies attracting each other “fall” to their common center of mass point. In case of the pebble and the Earth, the center of mass would be almost indistinguishable from the center of the Earth, which can therefore be considered at rest and the pebble falling to it.

Roughly speaking, the equality of a body’s inertial mass and its passive gravitational mass constitutes, essentially, the principle of equivalence, although these masses are equal, not equivalent. Exact equality of these masses was questioned since the observations leading to this conclusion were not all that accurate; it could be that this equality is only approximate and the difference is so small that it escaped detection in those experiments. Alternative observations made by more cleverly designed experiments also confirmed the equality of these masses and with a much higher accuracy establishing the conclusion.

It was discussed in [IV] that the energy and the inertial mass are equivalent, one and the same thing; i.e., energy produces inertia. The question arises if the energy is also equivalent to the passive gravitational mass, i.e., if the total inertial mass of a body is equivalent to its passive gravitational mass. Experiments conducted with the radioactive material provided the answer in the affirmative: Inertial mass of a body is always equal to its gravitational mass; i.e., the equivalence principle always holds true.

It follows from the equivalence principle that a body, e.g., a pebble, released above ground experiences a constant acceleration towards the Earth, denoted by g. Suppose that an observer is locked in an elevator where there is no gravitational field and the elevator is accelerating “upwards” with its acceleration being equal to g. The direction of the acceleration is called “upwards” here just for convenience, not with reference to the Earth. Now a pebble is released at some height above the floor of elevator. Then the observer would see the pebble undergoing the acceleration equal to g towards the floor. The observer would have no way of knowing whether the acceleration was caused by a gravitational force in the direction of floor or because the observer was in a non-inertial frame of reference, that of the accelerated elevator. Consequently, Einstein assumed that a gravitational field and the corresponding acceleration of a reference system are equivalent, i.e., being at rest on the surface of the Earth is equivalent to being inside a spaceship, far from any sources of gravity that is being accelerated, e.g., by its engines.

If the engines of the space ship are now stopped, the space ship will have no acceleration and thus, it would constitute an inertial frame of reference. Relative to the accelerated elevator, the elevator with no acceleration would also be equivalent to the elevator falling freely to the Earth in its gravitational field. It follows that free-fall is actually an inertial motion. Objects in free-fall do not really accelerate; i.e., free-fall and inertial motion are physically equivalent.

The principle as stated above is known as the weak or the Galilean principle of equivalence. Einstein assumed that the weak, Galilean, principle of equivalence is valid and that the outcome of any local non-gravitational experiment in a freely falling laboratory is independent of the velocity of the laboratory and its location in spacetime. With this modification, the principle is known as Einstein’s principle of equivalence. The Einstein equivalence principle has been criticized as imprecise, because there is no universally accepted way to distinguish the gravitational experiments from non-gravitational ones. The weak equivalence principle restricted to “small” bodies, i.e., valid locally, that do not experience self-gravitational effects combined with Einstein’s adjustment is known as the strong equivalence principle. Self-gravitational effects are largely responsible for the creation of the black holes as will be discussed.

Being based on direct conclusions of the experimental observations, the equivalence principle is empirical in nature. Some efforts have been made to deduce it using alternative reasoning but they remain controversial.

Geometrization of Gravitation

Newton’s first law of motion [II] states that a body moves with a constant velocity, i.e., along a straight line with a constant speed, termed a “uniform linear” motion, unless acted upon by a force. Existence of the “force” was postulated to accommodate the motion that deviate from a uniform linear one. First, let us focus on the uniform linear motion in the non-relativistic setting, i.e., motion in a “free space.” In this case, the Euclidean geometry is the underlying space geometry and time is the parameter. The first law of motion says that if two bodies with different masses are propelled with the same velocity from the same initial point, they will follow the same straight line maintaining the initial speed rendering the inertial mass of the moving body inconsequential. In the relativistic free space, the underlying geometry is the Minkowsakian but this assertion remains essentially the same with the “straight line” being its counterpart in the Minkowski space, which has about the same properties for the present purpose. For simplicity, the concepts will be clarified with the non-relativistic example.

A straight line is determined by any two points on it. The line-segment between the two points is determined completely by the geometric considerations: It is the shortest line segment between the two points; i.e., among all curves that can be drawn joining the two fixed points, the straight line segment is the shortest one, i.e., the extremal joining the two points. This segment can be determined purely by the geometrical means, i.e., without any reference to any “mechanical” concepts of physics. One can assign two fixed time values to the two end points of segment to fix the velocity. Thus, the motion in a free space is completely geometrized on the background of the Euclidean space.

Now, according to the equivalence principle, two bodies with different inertial masses propelled with the same velocity from the same initial point in the same gravitational field would follow the same trajectory. Taking a clue from Newton’s first law, the motion of a body in a gravitational force field should be determinable by the geometrical considerations alone, i.e., with no reference to the mechanical concepts of physics; particularly with no reference to some force field. It is natural to expect such a description of motion in a gravitational field to be an extension of the geometrized form of Newton’s first law, i.e., the trajectory should be expected to be an extremal in some space.

Now, the bodies in a gravitational field do deviate from a uniform linear motion in space. Hence the underlying space geometry cannot be Euclidean. In the special relativistic formulation, we need a Minkowskian spacetime, which is adequate for the inertial systems but not for the non-inertial ones that is the case here. In order to “extend” the first law of motion to accommodate gravitation, we need a richer geometrical structure in spacetime such that the counterpart of the straight line in it would provide the trajectory of a body in a gravitational field. If this can be done, then the concept of “force” can be dissociated from gravitation and thus, the motion can be described purely in geometrical terms.

The Galilean principle of relativity and the associated Lorentz transformations, which transform the coordinates between the inertial frames of reference, cannot be general enough to describe motion in the non-inertial frames; therefore, they should be extended to the geometries richer than the Minkowskian. Accordingly, Einstein extended the Galilean principle of relativity to the principle of general covariance: All frames of reference are equivalent for the formulations of the laws of physics, i.e., the laws, equations, of physics must be covariant with respect to all coordinate transformations, not just the Lorentz ones. Here the term “all” is used in the restricted sense, i.e., all that we hope to encounter.

We also need a geometrical structure sufficiently rich to be able to describe the motion in a gravitational field in its geometrized form, which Einstein assumed to be a Riemannian one. As mentioned in [IV], the Riemannian geometry in general was constructed by discarding the parallel lines axiom from the set of the founding axioms of the Euclidean geometry. Couple of simple examples of two dimensional Riemannian spaces are shown in Figure 1 below together with the Euclidean for comparison.

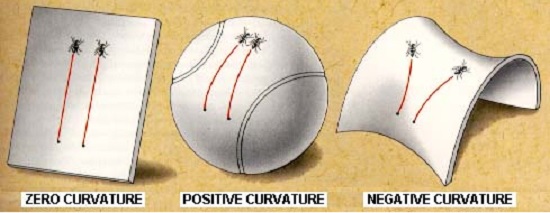
Figure 1: Examples of the Reimannian spaces

In a Euclidean manifold, shown on the left, two ants trace two straight parallel lines following their noses with the same speed. The Minkowski space does not differ from the Euclidean in any consequential way in the present context. Both of these are flat spaces, i.e., with zero curvature. The surface in the middle is that of a sphere together with the counterparts of the ants’ trajectories. This surface has a positive curvature. The picture on the right, that of a saddle, shows a Riemannian space with a negative curvature. Flat spaces are the special cases of the Riemannian, with zero curvature. The counterparts of the straight lines in the Riemannian spaces are called the geodesics.

After numerous detours and false starts, Einstein succeeded in 1915 in developing what are now known as his field equations. Equivalence of the inertial frames and free fall as well as some heuristic reasoning played a role in this development. These equations are used to determine the geometry of spacetime in the presence of a body and thus, gravitation is understood in terms of the geometry of spacetime. While we continue to use the term “field,” it refers to the corresponding geometry, i.e., the “gravitational field” of a body means the “geometry of the spacetime resulting from the presence of the body.” Motion of a body in this geometry was then determined by standard, purely geometric methods as a geodesic. Figure 2 illustrates the “distortion” to the geometry of the spacetime resulting from the presence of a massive body. The two curves show the geodesics.

Figure 2: Effect of a massive body on the geometry of spacetime.

Newton’s formulation describes the gravitational effects in terms of the force applied by the bodies on each other at a distance. Action at a distance was eliminated by introducing the concept of the “field,” the same way as was done in electrostatics. This theory is mechanical in nature. The general theory of relativity describes the gravitational effects in terms of the geometry of spacetime, which is a non-material, non-mechanical, non-physical manifold providing the background for the workings of nature. The geometry in spacetime is a structure constructed by the mind to describe our experiences pertaining to the gravitation. This brings us back to the ongoing question: What is reality? This geometric formulation indicates that our perception of the gravitation, which is all the reality there is, is essentially a construct of the mind.

Consequences of General Theory

Returning to the theory, only approximate solutions were obtained initially and some predictions were made. In 1916, the astrophysicist Karl Schwarzschild found the first non-trivial exact solution to the field equations, which provided the foundation for a great deal of further work. We discuss below some of the observable consequences of this formulation, which differ from what was expected from Newton’s theory of gravitation together with the laws of motion.

Time Dilation

One of the consequences of the geometric formulation of gravitation is that the processes close to a massive body run slower than the processes taking place farther away; this effect is known as the gravitational time dilation. While it is similar in nature to the time dilation of the special theory of relativity, which corresponds to the inertial frames, it differs since the underlying geometry is a curved Riemannian one with the corresponding frame being non-inertial. Frequency of a light wave is the inversely proportional to the time period. This time dilation in case of the light in a gravitational field implies that the light travelling towards a stronger gravitational field is blue-shifted and that travelling towards a weaker field is red-shifted. Also, the light responds to a gravitational field much like a massive body travelling along the corresponding geodesic, called the null geodesic, bending towards the gravitating body. The null geodesics are the counterparts of the straight lines along which light travels in the free space. Both of these effects are shown in Figure 3.

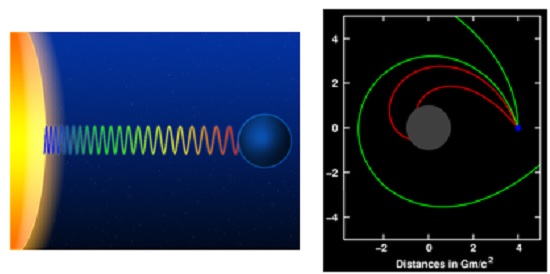
Figure 3: Response of light to a gravitational field
The figure on the left shows the light frequency shift
and the one on the right shows the bending of light trajectories
in the gravitational field of the body shown in grey.

Gravitational red-shift has been measured in the laboratory. Gravitational time dilation in the Earth's gravitational field has been measured using the atomic clocks. All results are in a close agreement with the predictions of the general relativity.

Experimental verification of the bending of light in a gravitational field has some interesting political overtones. The First World War was still on and Eddington was a conscientious objector equipped with a scientific reputation and a strong personality. There was a rare opportunity to test the bending of light in the gravitational field of the Sun during a total solar eclipse in Africa in 1919. This effect is noticeable only during eclipses, since otherwise the Sun's brightness prohibits a discernible observation. Frank Watson Dyson, who was to be a companion of Eddington in the expedition argued, for the indispensability of Eddington’s expertise in conducting the test that allowed him to escape prison during the war. It is said that Eddington did sign the letter requesting for a waiver from the military service but noted that even if he was not needed for the test he would not have served in the military. The war was concluded while the preparations for the expedition were still continuing. Eddington travelled to the island of Príncipe near Africa to observe the solar eclipse of 29 May 1919.

Figure 4: One of Eddington's photographs of the total solar eclipse of 29 May 1919.

Eddington showed also that Newtonian gravitation could be interpreted to predict half the shift predicted by Einstein. It was Einstein’s prediction that was in agreement with Eddington’s observations placing the general theory of relativity on a strong footing and shooting Einstein to fame.

Orbital Effect

As was mentioned in [III], planets revolve around the Sun in elliptical orbits in conformity with Newton’s formulation of gravitation and his laws of motion. Accordingly, the orbit of a planet is a fixed ellipse. According to the general relativity, the geodetic path of a planet in the geometry corresponding to the Sun is not a fixed orbit; instead, the point of its closest approach to the center of mass, which is almost at the center of the Sun, would shift. Consequently, the “orbit” is a rotating ellipse as shown in Figure 5.

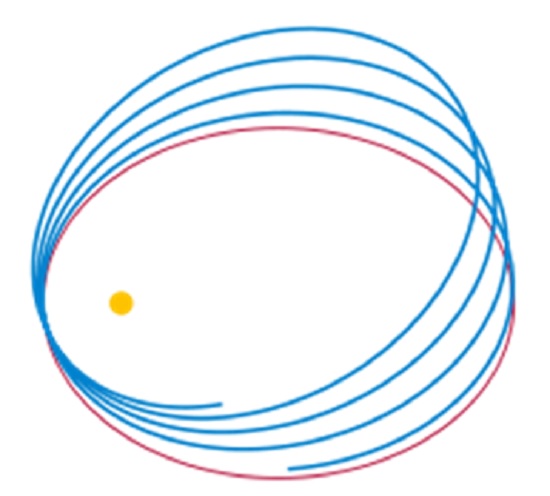
Figure 5: Newtonian (red) vs. Einsteinian orbit (blue) of a planet orbiting the Sun

This phenomenon, perihelion shift, had been observed for the planet Mercury by Le Verrier in 1859, which was explained qualitatively and confirmed numerically by the general relativistic calculations. Since the field equations were deduced by heuristic reasoning, one could not be sure of their ability to yield the correct geometrical structure of the spacetime. This agreement between the calculation and observation essentially established the correctness of the field equations.

Black Holes

A black hole is a region of spacetime from which nothing can escape, including light; hence the name. The likelihood of the existence of black holes was suggested by John Michell in 1783. Later Laplace promoted the same idea. These suggestions were ignored for it was assumed that light being massless could not be influenced by gravity. As discussed above, general relativity predicts that light does respond to gravity, which has been verified experimentally, invalidating the corresponding argument.

In 1931, based on his calculations Subrahmanyan Chandrasekhar showed that certain bodies with mass exceeding 1.4 solar masses, now called the Chandrasekhar limit, have no stable solutions causing collapse of the body. Phenomenologically, the collapse is caused by the self-gravitation of the body. i.e., a body’s center attracts its peripheries. It is said that just before Chandrasekhar was going to present his paper in a conference, he discussed it with Eddington who in turn had the time allotted for his presentation increased using his influence. Chandrasekhar was very much encouraged. Eddington had also had himself placed to speak following Chandrasekhar. After Chandrasekhar finished his presentation, Eddington tore into it. Someone remarked later that it was not nice of Eddington to embarrass a young physicist in this manner, after even leading him on, at which Eddington replied that the young physicist should be thankful to him for allowing him more time to present his work. There were others who objected to Chandrasekhar’s arguments but the black holes were here to stay. Robert Oppenheimer and others predicted later that neutron stars above approximately three solar masses, the Tolman–Oppenheimer–Volkoff limit, would collapse into black holes for the reasons presented by Chandrasekhar. After a black hole has formed it can continue to grow by absorbing the mass from its surroundings.

Figure 6: Simulated view of a black hole (center).

Figure 6 shows a simulated view of a black hole under realistic conditions. The defining feature of a black hole is the appearance of an “event horizon,” a boundary in spacetime through which matter and light can only pass inwards to the black hole. Nothing, not even light, can escape from inside the event horizon. As predicted by general relativity, the presence of a mass deforms the spacetime. At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.

By their very nature, black holes are impossible to detect directly. However, a black hole's existence can often be inferred by observing its gravitational interaction with its surroundings. There is now ample evidence of the existence of the black holes, including the supermassive ones in the centers of most galaxies, which are believed to have been caused by very massive stars formed by the big bang.

Gravitational Waves

General relativistic field equations predict the existence of the “gravitational waves,” analogous to the electromagnetic waves. As gravitation itself, these waves are understood geometrically as the ripples in spacetime propagating at the speed of light, not as the “mechanical” waves.

Since Einstein's field equations are non-linear, arbitrarily strong gravitational waves do not obey linear superposition, rendering them somewhat different from the electromagnetic waves and making their description difficult. However, for the weak fields, a linear approximation can be made. Such linearization is sufficiently accurate to describe the exceedingly weak waves that are expected to arrive here on Earth from far off cosmic events. The simplest type of such a wave can be visualized by its action on a ring of freely floating particles.

Gauge Geometries

Although the global parallels do not exist in the Riemannian spaces, they have parallels locally. For example, finite number of small flat squares can be joined to construct maximal and minimal surfaces included in and enclosing, respectively, to approximate a spherical surface. As the number of the squares is increased and thus their size reduced, both surfaces would tend towards the spherical surface. Clearly, the parallels can be defined on the squares. In this sense, the Riemannian spaces are locally Euclidean and the concept of parallel transport can be defined in them.

In the flat spaces, a vector parallel transported remains the same everywhere but in the curved Riemannian spaces, it changes. For example, if a ship travels along the equator without twisting, then a flag pointing towards a pole at the start will not be pointing to it as it travels. Thus, a vector parallel transported around a closed loop in a curved space, does not return to the original one upon its return. However, the length of the vector remains the same everywhere.

After the geometrization of gravitation, Hermann Weyl attempted to bring electromagnetism in the framework of geometry and unify it with gravitation. To this end, he postulated that the length of a parallel transported vector also changes to develop his geometry with a richer structure than the Riemannian. Weyl proposed precise rules for this change. As a consequence, he argued further that a universal measure of length, gauge, cannot be assigned to a space; instead a gauge can be assigned essentially arbitrarily at every point in the space; thus endowing mind to have even greater intervening influence on the perception of reality. The construction is now known as a “gauge transformation.” With these transformations, Weyl deduced two of Maxwell’s equations. The transformations involve some functions, which were identified with the electromagnetic potentials, termed the gauge potentials. In spite of this encouraging development, his construction did not lead to a unification of the gravitational and electromagnetic fields, but it did bring electromagnetism within the grasp of geometry and impacted heavily on the later theories of physics; so much so that the gauge transformations are at the heart of the modern fundamental theories of physics. As a result of this construction, electromagnetism was dubbed a “gauge field.” In view of the resulting geometry, electromagnetism is identified with a circle. The concept has been extended to other Gauge fields, e.g., the weak and strong, which were discovered later in the post-classical formulations.

Kaluza approached the issue of unification of the fields somewhat differently. He extended the four-dimensional spacetime used to accommodate gravitation to five-dimensional Riemannian space using the electromagnetic potentials to define its structure. Later Klein made some contributions to the final formulation. In time, this formulation was extended to still higher dimensions to accommodate the multi-dimensional gauge fields. While no unique trajectory can be assigned to a particle in the Weyl space, a particle’s path in the Kaluza-Klein space is a unique geodesic, although in a higher dimensional space than the four-dimensional spacetime. Weyl retained the dimensionality of specetime but altered its structure; Kaluza-Klein retained the Riemannian structure but increased the dimensionality. Earlier Lorentz had described the trajectory of a charged particle in the Minkowski spacetime endowed with an electromagnetic field using the relativistic extensions of Newton’s laws. Kaluza-Klein geodesic is essentially the Lorentz trajectory. However, this derivation brings electromagnetism into the fold of the Riemannian spaces. Yet again, Kaluza-Klein formulation did not succeed in unifying the electromagnetic and gravitational fields, but came to constitute a crucial structure underlying the modern fundamental theories of physics. In fact, Weyl’s and the Kaluza-Klein frameworks complement each other. Following the Kaluza-Klein formulation, attempts were made to formulate gravitation also as a gauge field. Such attempts remain unsuccessful so far.

Concluding Remarks

The geometrical formulation of gravitation discussed in the present article is founded upon the observed equivalence of the inertial and gravitational masses. Geometric structure of the spacetime in the presence of a body is determined from Einstein’s field equations, which are arrived at by mostly heuristic reasoning. The resulting structure is a curved Riemannian one, differing from the flat Minkowskian, which is the structure in the absence of the body. This difference is often expressed as the “deformation” of the spacetime caused by the body. As commented before, the “deformed” structure is constructed to describe the phenomena resulting from presence of the body. Various predictions of the resulting theory are in a closer agreement with the observations than those of the earlier ones establishing it as a better representation of the workings of nature. Only a few have been described here to impart an understanding of the major impact of the geometric theory.

Geometrization of gravitation initiated a metaphysical paradigm shift in formulating the theories in physics contrasting with the earlier mechanical thinking, essentially by eliminating the concept of force. Earlier thinking was that it was the force experienced by a body that was pulling it towards the body applying the force. In the geometrical formulation, the moving body moves along its natural path in spacetime defined by the geometric structure resulting from the presence of the gravitating body.

Geometrization and unification of the workings of nature had a metaphysical appeal that motivated geometrization of electromagnetism and unify it with gravitation. Although the unification attempts did not succeed, electromagnetism was brought in the geometric fold giving rise to the concept of gauge fields, which are geometric in nature, e.g., electromagnetism is identified with a circle. The gauge theoretical formulation itself has some appealing features, which motivated efforts to formulate gravitation also as a gauge theory, which too did not succeed. However, a composite structure was constructed successfully by forging the gravitational Riemannian structures and the gauge fields, which constitutes the underlying geometric structure of the modern theories in physics. When gravitation is not of importance, which is mostly the case, the Riemannian base manifold is replaced with the Minkowskian that retains the basic nature of the composite structure.

Acknowledgement
The images incorporated in this article are the courtesy of Wikipedia.org.