Quantum Theories: Multiple Paths

The “paradox” is only a conflict between reality
and your feeling of what reality “ought to be.”
— Richard Feynman

As discussed in the article “Perceptions of Physical Reality: Quantum Theories – Founding Developments,” physicists faced an enigmatic, paradoxical, situation: A physical entity classified either as a particle or a wave in the classical thinking, is both, a particle and a wave; which was forged into the doctrine of wave-particle duality and made the foundation of quantum mechanics. This observation was demonstrated most clearly in the double slit experiment. In the present article, I will describe the observations in this experiment in more detail to acquire deeper insight, followed by the related developments in the theories of mechanics.

Passage through Double Slit System

Basic double slit arrangement is shown in Figure 1:

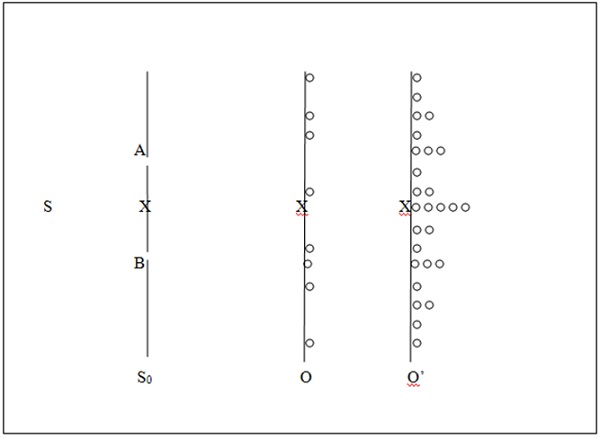
Figure 1. Basic double slit experiment

In Figure 1, S is a source of the entities, which encounter a screen S₀ with slits A and B in it followed by an observation screen; O and O’ are the copies of the same observation screen, with O showing the individual arrivals and O’, after many have landed on it, which can be and often is an array of particle detectors. The experiment can be conducted with one entity at a time by reducing the intensity of S to a point that an entity is emitted from S after the previous one has landed on O, O’. The density pattern at O’ is symmetrical about the central point X. This is all that is available to the observer; what happens in between the slits and the observation screen is not.

Initially, the observations were made with a multitude of the entities. What was observed was the density pattern of O’, which resembles the intensity distribution of two interfering wavelets, which constituted the basis of the concept of wave-particle duality. For comparison, the density pattern expected of the particles travelling according to the classical law of motion is shown in Figure 2, which is the same as Figure 2 in “Perceptions of Physical Reality: Quantum Theories – Founding Developments;” except that the particles arriving via slits A and B are now labeled by PA an PB, respectively.

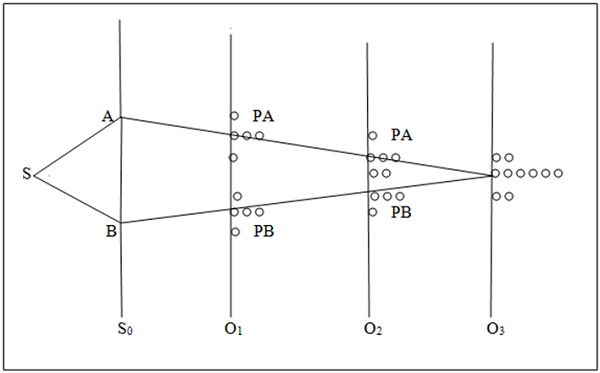
Figure 2. Double slit experiment with classical particles

In this experiment with the entities such as photons and electrons, each individual entity is registered as a single particle, i.e., captured instantaneously by one of the detectors with a vanishingly small aperture, that can be idealized by a point, at all locations of the observation screen, as shown in Figure 1. While the entity is detected as a particle, its location on O, O’ is not necessarily what is expected on the basis of the classical law, which is the central point; instead, one after the other, they arrive at different, apparently random, locations as indicated on O in Figure 1. After many have arrived an interference-like density pattern immerges as indicated on O’. Thus, the individual arrivals are not completely random; wave-like coherence is built in them.

Pertaining to the classical law governing the motion of particles: Newton’s first two laws are covered by the action principle, as discussed in the article, “Perceptions of physical reality: Classical Theories – Particle Motion;” and the third law does not add to the description of particle motion. Therefore the classical law governing the motion of particles will be considered to be the action principle.

As observed in the double slit experiment, the density on the observation screens is different from the sum of the densities emanating from the slits A and B individually: If one of the slits, e.g., B, is closed, then the individuals arrive at the classically determined location, which also assumes that they travel along a straight line. Similar density pattern results if A is closed and B is left open; the sum of the two densities is like that on O₃ in Figure 2; which is different from that on O’ in Figure 1, which is what is observed with both slits open.

What has changed from two slits open to one slit open is that with one slit open, one can determine which way the entity came, which confines it to the corresponding slit, and thus identifies it as a particle. One still does not know the path; all one knows is that it came from slit A, if this is the one open. From this, one concludes that it is a particle and therefore one can use the classical law for particle motion to determine its location upon arrival; the action principle assigns also a straight line path to the entity. “Which path” term is used in literature to express this state of affairs.

In the efforts to reconcile the dual nature, it was suggested that these entities are particles individually but wave in a collection interfering with each other. Aside from the difficulty that such interference would infringe upon their isolated nature, observed behavior of the individuals in Figure 1, renders this suggestion untenable: Wave-like coherence is inherent in the behavior of each individual entity, which shows up only if both slits are open. Thus, if one slit is open, the entities behave like classical particles; they travel along classically determined trajectories and arrive at classically determined locations; if both slits are open, each entity behaves like a wave. If “which path” information is available, the entity behaves like a classical particle; otherwise, it behaves like a classical wave.

The question arises: Does one individual entity pass through one of the slits or both when both slits are open? If it passed through one of the slits, A or B, selected randomly, i.e., about half of them passed through each slit; the resultant density should be the sum of the densities corresponding to the slits individually, which it does not. One can only conclude that if both slits are open, the “particle” passes through both slits and interferes with itself; otherwise, it passes through one slit and behaves as a particle.

One can leave both slits open and yet determine the particles that passed through one of the slits, e.g., A, by watching them behind S₀ somewhere along the path from A to the point of arrival on O, O’ after they have passed through A. This can be done by installing a detection device along the path. In case of the entities being the electrons, this detection device can be an arrangement to scatter the photons from them. If a scattered photon is observed, there is an electron there. There are detection devices available for every entity, which can be used. Result is the same: If the entities are detected, they are detected as particles and behave as classical particles in every way. Such an observation about A affects also the entities passing through B, which also behave as particles as a result of the observation behind A: Interference-like density pattern disappears; classically expected distribution of the particle density results.

Above observation can be made also by collecting the entities coming from one of the slits and ignoring the others; similarly the entities coming from the other slit can be determined. The result is again the same: Entities arrive as particles and the sum of the two produces the classically expected pattern. If one collects all the entities regardless of which way they came, the density pattern resembles the interference pattern. A simple way to determine which way certain entities came is to move O, O’ towards the slits from the position O₃ of Figure 2 where an interference-like density pattern is observed, to the positions of O₁ and O₂; the interference-like distribution disappears slowly to yield the corresponding density distributions shown in Figure 2, which is expected of the particles.

The conclusion of the above observations is that if the entity is watched; equivalently, if “which path” information is available, it is a particle; otherwise, it is not; then it is a wave. Philosophers had amused themselves by posing questions like, “Is moon there when not looked upon?” Physicists working with regular instruments now face such questions, and the answer appears to be that it is not.

Above experiment can be conducted with photons that originated somewhere billions of years back; encountered a galaxy, which acted like a gravitational lens, then arrived on Earth and then observed. If one collects the photons coming along one of the two ways, it acts like a classical particle; if one collects all coming along both paths, it acts as a wave; as if each photon knew billions of years back how it would be observed.

It has been argued that these entities have no form until observed, i.e., they acquire form upon observation and the form depends on how it is observed, i.e., if the observer decides to observe a particle, a particle is observed; if the experiment is set up to observe a wave, a wave is what is observed. Thus, observer has the decisive role in defining the physical reality.

Data can be collected in one experiment that can be divided into sets with one set containing the “which path” information and then combine it with another set to erase this information, which is called the quantum eraser. If the data with “which path” information is examined, the entity is a particle; if the data where “which path” information is not available is examined, one observes a wave. It appears that these entities have no definite form even after they have been observed as having a form.

Practicing physicists have indulged in devising clever ways to observe the entities as particles, determine “which path” it took, and retain its wave character, but to no avail so far. Number of such experiments with pertaining discussion can be found, e.g., in the article: J. Horgan, Quantum philosophy, Scientific American, 1992 July issue, pp. 94-104. According to Feynman, the double slit phenomenon is the “only mystery of quantum mechanics;” which is: Why do the “particles” behave the way they do in the double slit experiment. Related issues will be revisited in the subsequent articles. For now, I describe the developments resulting from such observations.

Feynman’s Multiple Path Formulation

Feynman is known to introduce his multiple path formulation of quantum mechanics, technically known as the path-integral formulation, with the following statement:

Will you understand what I’m going to tell you?
…No, you’re not going to be able to understand it.
… I don’t understand it. Nobody does.
— Richard Feynman on Path Integrals

Not a very encouraging introduction and that too by the author of the formulation. However, this formulation has introduced a metaphysical element to an otherwise empirical formulation of quantum mechanics; has provided some insight into the workings of quantum mechanics; and has proven to be a remarkable method to tackle variety of topics and problems. Nevertheless, some mysterious elements do remain inherent in this formulation.

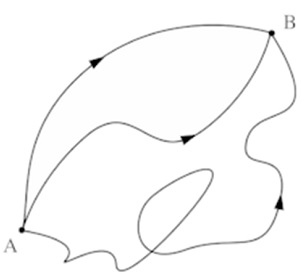
Figure 3. Three of Feynman’s paths from A to B

As discussed above, the inescapable outcome of the double slit phenomenon is that a “particle” travels along more than one path if they are available to it. Dirac had noticed that from the structure of the wavefunction it appears that it is constituted of the contributions from a multitude of paths as if the particle has travelled along many trajectories to reach the region of observation. Motivated by the observation in the double slit system and spurred by Dirac’s observation, Feynman postulated: A particle travels along all alternative paths available to it, termed the “interfering alternatives,” in his terminology. In fact, in about every situation, there are infinitely many paths available to a particle, e.g., in the double slit system, even if there is only one slit open, there are infinitely many trajectories joining the slit and the point of observation that are available to the particle; notice that the paths are not necessarily classical particle paths. Three typical trajectories for a particle reaching B from A are shown in Figure 3. In fact, in quantum mechanics, one can talk of small neighborhoods of the points, not the points. Feynman assumed further, that each path has its own amplitude attached to it, called the phase-factor, calculated in terms of the classical action; and the wavefunction is the equiweighted sum of all of these amplitudes. From these assumptions, Feynman succeeded in deducing about the complete structure of quantum mechanics, except that he assumed validity of the Born rule to calculate the probability densities.

The formulation discussed in “Perceptions of Physical Reality: Quantum Theories – Founding Developments;” is essentially empirical arrived at by intuitive reasoning and heuristic methods. Feynman’s formulation introduced a metaphysical element to it: Particle travels along trajectories, albeit infinitely many. Also, a procedure is developed to construct the wavefunction in a systematic manner. A significant element of this formulation is that it relates quantum mechanics with classical mechanics by way of calculating the phase factors in terms of the classical action, while the earlier formulation is almost completely disjointed from the classical theories except for the postulated analogies.

Feynman himself is known to be leaning towards the particle interpretation of these entities, which appears to reflect in the observations in the double slit experiment. However, the menacing wave element remains: Particle takes all paths, not one path picked randomly out of many and it carries its own wave amplitude with it, i.e., each path represents essentially a wave and the Feynman sum is just the superposition of infinitely many waves. Thus, something has been gained, but not a great deal, in the fundamental sense.

Formulation in Weyl’s Geometry

We recall the basic elements of the Weyl geometry discussed in “Perceptions of physical reality: Classical Theories – Geometrization.” Weyl postulated that the length of a parallel transported vector changes according to a prescribed rule and one can assign a measure of length essentially arbitrarily at every point in space. This construction is now known as a “gauge transformation.” Referring to Figure 3, a vector transported from A to B experiences a change in length, which depends on the trajectory followed. This gauge transformation determines the length of a vector at B in terms of its length at A, which depends on the path, termed the “natural gauge.” In addition, a measure of length can be assigned at A and B independently as well as all other points, which is termed the “assigned gauge.” There is a rather fuzzy separation between the natural and assigned gauges, which we omit for its rather technical nature, and it is of no consequence here.

Wheeler argued that due to an arbitrariness of the assigned gauge, one cannot assign a unique trajectory to a particle, e.g., by the classical action principle, since the value of action can be changed by altering the assigned gauge. Therefore, one must assign all trajectories from one point to the other to a particle. Since there are infinitely many trajectories assigned to a particle, its physical attributes can only be some aggregates over the trajectories. In the Weyl geometry, such aggregates can be expressed as integrals paralleling Feynman’s path integrals. However, instead of the phase factors of Feynman, Wheeler’s form has gauge factors calculated from the so called gauge potential with no wave-like attribute and no relation to the classical action. Wheeler then replaces the gauge potential with the infinitesimal classical action but they still do not possess a wave-like attribute. In the non-relativistic approximation, Wheeler obtains a diffusion equation, which had been used by Nelson to deduce the Schrödinger equation by introducing the wave-like attribute.

While Feynman postulated multiple trajectories for a particle and assumed that the wavefunction is the sum of phase factors over these paths, Wheeler assigned multiple trajectories for lack of a unique one and deduced parallel results from the properties of the Weyl geometry including the form of the aggregate. Wheeler is ambiguous about the factors to be summed rendering the formulation deficient in deducing much of the the formulation of quantum mechanics, although Wheeler’s form does lead to the Born rule, which Feynman’s form does not; Feynman assumed it externally. Also, the assigned gauge appears explicitly in Wheeler’s form together with the natural gauge. In Feynman’s formulation, there is no concept of the gauge transformations; consequently, there is no factor paralleling the assigned gauge in the formulation.

Primal Foundations of Mechanics

Consider the observations shown in Figure 1. Individually, the entities are observed as having small extension in space and time that can be idealized by mathematical points; i.e., particles, by definition. However, they do not arrive on the observation screen at the locations determined by the classical law for the motion of particles. Thus, the two assumptions put together that (the entity is a particle at all space-time points and the classical law of motion for a particle is valid) contradicts the observation. According to a basic principle of logic, if an assumption implies a contradiction, the assumption is false. In the present context, this means that the assumption (the entity is a particle at all space-time points and the classical law of motion for a particle is valid) is not true. This can occur in three ways:

The entity is not a particle at some space-time points but the classical law for particle motion is valid;

The entity is a particle at all space-time points but the classical law for particle motion is not valid;

The entity is not a particle at some space-time points and the classical law for particle motion is not valid.

As discussed above, if an entity is observed at some points as a particle, then it is assumed that it must travel according to the classical law governing the motion of particles. Quantum mechanics is founded on the assumption that the classical law of motion for a particle is valid; it is just that the entity is not a particle at some space-time points; wherever it is a particle, its motion is described accurately by the classical law; where it is not a particle, this law become irrelevant. Thus quantum mechanics is founded upon Premise #1. It is assumed further that in the space-time regions where the entity is not a particle, it is a wave and travels according to the classical law for the propagation of a wave. The two forms are then forced to “coexist” by forging the doctrine of wave-particle duality. This uneasy coexistence of mutually contradictory attributes is employed to explain the observations of Figure 1.

If an entity can be confined to a small region identifying it as a particle, it is found to conform closely to the classical law of particle motion. This observation is only approximately true and can be “described” even if the entity is a wave as is the case with light in which case the wave theory is used to explain the observation that light travels along almost straight lines due to small wavelengths.

If Premise #2 can be shown to yield a “satisfactory” theory, then Premise #3 would become irrelevant. Besides, Premise #3 is covered in parts by Premises #1 and #2. Thus, it is more reasonable to explore Premise #2 before considering the Premise #3. Developments based on Premise #2 are discussed in the following section.

Motion of Particles

In spite of some leaning towards the particle picture, Feynman’s path-integral formulation of quantum mechanics still incorporates the wave nature. Wheeler’s formulation is unclear on this point. Recently, there have been some developments based on the assumption that the physical entities are particles everywhere and always, and seek to develop a law for particle motion different from the classical one, i.e., to develop a theory of mechanics founded upon the Premise #2. As discussed above, no wave is ever observed; inference of their wave nature is arrived at by the resemblance of the density distribution in Figure 1 with the interference pattern of a wave, which is a tenuous assumption from the outset. Other phenomena supporting the wave nature are essentially equivalent to the double slit phenomenon. Furthermore, these entities whenever they are observed, are observed with small extension in space-time and isolated from each other, i.e., as particles. Thus, the Premise #2 is about the strongest hypothesis to base a theory of mechanics on. In this section, we discuss some developments in this direction.

As discussed in the article, “Perceptions of physical reality: Classical Theories – Particle Motion,” Hamilton’s Action Principle can be used to characterize the classical path for a particle to follow between two given points. The classical law of particle motion is clearly approximately accurate; deviations from this law are observed at a very small, “microscopic,” scale. Yet again, if the law of classical mechanics is invalid for the “microscopic” entities, they are invalid for all; it is just that the deviations for them are too small to be noticed in the observations pertaining to the “macroscopic” entities. “Microscopic” and “macroscopic” terms are used for convenience, understood as follows: If the associated action is of the order of Planck’s constant, which is equal to about 6.63 × 10^-34 m² kg / s, then the phenomenon is called “microscopic;” if it is large in comparison, then it is “macroscopic.”

Since the classical criterion for the motion of particles, the action principle, is approximately accurate, some adjustment to it might lead one to a better law of particle motion. To this end, we reformulate the action principle in terms of Weyl’s gauge transformations.

Referring to Figure 4, consider the trajectories from a point A to another point B, with ACB being the classical particle path to be determined. The action principle states that the action along all other paths, e.g., ADB, AEB, in an arbitrarily small neighborhood of ACB, is almost the same as along ACB. The term “almost” has a precise mathematical meaning in this context. The action principle determines the classical particle trajectory with given points A and B uniquely.

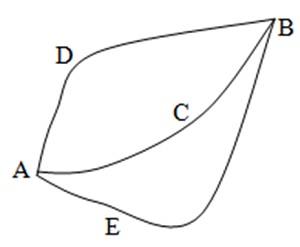
Figure 4. Trajectories from A to B

The action along an inverted path is negative of the original path, e.g., the action along BDA is negative of the action along ADB. Consequently, the action principle is equivalent to requiring the action along all closed paths, e.g., ACBDA, AEBCA and AEBDA, to be almost equal to zero. Thus, the action principle can be stated as follows: The action along all closed paths enclosing an arbitrarily small area with A and B being the fixed points on their boundaries is almost equal to zero.

As discussed above, the gauge transformations are generated from the “Weyl potential,” which is a function defined on the trajectories. A gauge transformation is the exponential of a constant multiple of the Weyl potential integrated along the trajectory. Wheeler took infinitesimal classical action multiplied by a constant to be the Weyl potential. The corresponding gauge transformation associated with a trajectory is just the exponential of a constant multiple of the action along the trajectory. With this, the Action Principle can be stated as follows: The gauge transformation generated by the action associated with all closed curves enclosing an arbitrarily small area with A and B being the fixed points on their boundaries is almost equal to one.

Recall that the gauge transformation associated with a trajectory transforms the length of a vector at a point X into the length at another point Y where the vector is transported along this trajectory from X to Y. For example, referring to Figure 4, the length of a vector transported along ADB at B is the length at A multiplied by the corresponding gauge transformation. We assume that the generator of the gauge transformation, and thus of the change in length, is the classical action as described above, without further mention.

It follows from the above that the Action Principle is equivalent to: “The length of a vector transported from a point A along any of all closed curves A to B to A, enclosing an arbitrarily small area with A and B being the fixed points, acquires a value, which is almost equal to its original value. For example, transport a vector of unit length at A along any of the closed curves, e.g., AEBDA in Figure 4; then the length of this vector is almost equal to unity as it returns to A. This characterization determines the unique classical trajectory for a particle motion from A to B.

The action principle admits a natural extension, the Action-Gauge Principle: A particle follows a trajectory along which its length returns to its original value somewhere along this path. This is an extension of the action principle as a criterion, on two counts: All curves, closed and non-closed, are taken into consideration; and the length resumes its original value exactly, not just “almost.” There are other issues pertaining to the extension, which we omit as they are not so relevant. It does not matter much how the “extended” criterion was arrived at for no matter how, it still would constitute a postulate as is the action principle itself, and this is how it should be taken: A postulate describing the motion of particles. An extension is an extension, a concept concocted by mind; not a derivation.

Clearly, the action gauge principle is a stability criterion for the particle motion, i.e., on the whole a particles maintains the dimensions associated with it along the trajectory it follows. To avoid confusion that may arise, the trajectories assigned to a particle by the action-gauge principle will be termed the physical trajectories. Smallest physical trajectory for a particle will be termed the “elemental path.” In standard units, the action associated with an elemental is of the order of the Planck constant, which is miniscule in comparison with the dimensions of our day to day experience even in a laboratory where quite miniscule quantities are encountered.

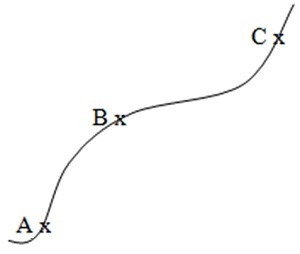
Figure 5. Physical paths

To illustrate, consider the trajectory in Figure 5. A particle follows a trajectory such that a vector of unit length at A transported along the trajectory transforms in a vector of unit length at some point B, and then again at C, and so on. If the particle travels along this trajectory, then it can reach B from A, but not any point in between. However, there are other trajectories which can take the particle at any given point on AB. This introduces a precision limit on the position of the particle, which is the origin of the uncertainty principle. We omit further details.

We have shown a non-closed path here. Such paths are termed “monotonic,” i.e., the action either increases or decreases along the path. A closed path is a continuing union of two monotonic paths, the union being a non-monotonic path, which will be discussed as encountered.

Assigned gauge clearly alters the particle trajectory. To illustrate: Consider the path AB with A being the initial point and B being the terminal point, and the assigned gauge, i.e., the unit of length, being the same at points A and B. If the path AB is allowed for a particle, then the length of a vector at B is the same as at A. Now, let the assigned gauge at A be the same as before but different at B. Then the length at B, in general, would be different from its value at A. Consequently, a different trajectory would satisfy the criterion set out by the action-gauge principle. Thus, the action-gauge principle defines the particle trajectories for a fixed assigned gauge distribution in space.

In his mathematical construction, Weyl had assumed the assigned gauge to be essentially arbitrary. For the physical systems, particle trajectories in the present context, it is assumed further that the values of the assigned gauge at physically equivalent points are equal; otherwise not, which is the second assumption of this formulation; the first one being the action-gauge principle. If all the points in space are physically equivalent, the assigned gauge is a constant, which can be taken to be the unit. For example, for a free particle, the assigned gauge can be taken to be equal to one along any trajectory it may follow as well as elsewhere in space-time. Now consider the particle passing through a slit and detected by a particle detector some distance away. The particle goes through an interaction at the slit and a different interaction at the detector. Thus, the assigned gauges at the slit and at the detector are different from each other and both are different from one, while at all the other points on any trajectory it may follow between the slit and the detector, it is equal to one.

Weyl’s gauge transformations associated with the trajectories possess the following useful property: If the values of the assigned gauge are identical at the initial and the terminal points of a trajectory, they cancel each other out; and if a trajectory is a continuing union of two paths, then the value of the assigned gauge at their common point also becomes ineffective. The values of the assigned gauge at such points can be considered to be equal to one. For example, the assigned gauge can be ignored for closed paths, e.g., the action principle and closed orbits of Bohr, as well as at the point B in Figure 5. Other examples will be considered as they arise.

Weyl had taken the constant multiplier in the exponent defining the natural gauge transformation to be real. London in 1927 took it to be purely imaginary arbitrarily to show an essential equivalence of an extended wavefunction with the Weyl length of a vector attached to the particle. Adler used the Weyl-London gauge transformation together with a stability criterion to obtain the Bohr quantization of the orbits of hydrogen-like ions. The present characterization of the particle trajectories, the action-gauge principle, has been shown to yield London’s assumption, which is a remarkable result. With this result incorporated, Wheeler’s formulation reduces to Feynman’s except that now the assigned gauge enters into the Feynman sums explicitly.

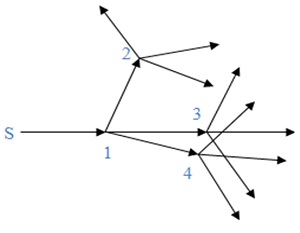
Figure 6. Microscopic physical paths

The action-gauge principle assigns infinitely many trajectories to a particle, which is an assumption in Feynman’s formulation and an intuition based deduction in Wheeler`s formulation. Also, in Feynman’s formulation, the “particle” is assumed to travel along all trajectories; Wheeler is mute on this point. According to the present formulation, the particle travels along one trajectory, selected randomly out of infinitely many. A particle trajectory is constituted of elemental paths; thus the particle travels in steps of the elementals, selecting each one randomly. It is clear that, a particle retains its particle attributes. In spite of this, the formulation introduces wave-like coherence on the “microscopic” trajectories, as illustrated below for a free particle, i.e., with unit assigned gauge, together with the mechanism of the particle motion as stated here.

Referring to Figure 6, S is a source of the particles. Infinitely many paths are available to an emitted particle in all directions. The particle takes one of them selected randomly. Here we have shown just one straight line elemental path, from S to 1, which is a classical trajectory for a free particle, restricted by the action-gauge principle, i.e., this is the smallest trajectory such that a vector of unit length at S transported along it has unit length at 1 also. Momentum of the particle along this line is constant and the action is equal to the momentum multiplied by the distance, which is of the order of Planck’s constant. This action determines this elemental path for the particle. Particle can reach any point on the sphere centered at S with radius equal to this length travelling along a straight line. The particle cannot reach a point in the interior of the sphere via a straight line path, but there are other trajectories that can facilitate its passage to each given point; all one requires is that the action along the trajectory be the same as along the line S to 1.

At 1, again the particle has infinitely many paths available; three straight line paths are shown in Figure 6, with terminal points 2, 3 and 4. Again, a path is selected randomly. Above comments apply to these trajectories also. Each of the terminal points, 2, 3 and 4, becomes the origin of the next set of trajectories. This parallels Huygens’ construction for the wave propagation.

It has been shown from the action-gauge principle that a particle trajectory of classical, large, extension, i.e., with “macroscopic” value of the action, is almost the same as assigned by the action principle, i.e., a classical path, regardless of the value of the assigned gauge, which has negligible impact at a large scale. This is yet another remarkable result, which is in agreement with the observations. This derivation requires some mathematical calculations, which is therefore omitted. Basic concept is that the action changes by a small amount near the classical trajectories of large extension, physical or not; such trajectories can be adjusted slightly to find a physical one, yielding a large number of physical trajectories in a small neighborhood of a classical trajectory. On the other hand, the action changes by a large amount about the non-classical trajectories, requiring a large adjustment to find the physical trajectories. In Feynman’s formulation, this result is obtained in about the same way as for the wave theory of light, which travels along almost straight lines. In both cases, this result is deduced using the interference properties of the waves; although it uses the same properties of the classical paths as the deduction for the physical trajectories. The derivation for the physical trajectories does not invoke any properties other than the particle attributes of the entity.

Physical Measurability and Wavefunction

Due to an arbitrariness of the assigned gauge, lack of uniqueness is an inherent characteristic of the quantities in the Weyl geometry for the value of a quantity can be altered by altering the assigned gauge. For this reason, Wheeler’s amplitude is also not unique. For lack of uniqueness, the concept of physical measurability cannot be assigned to the amplitude. Wheeler then constructs its “conjugate” and combines the two to construct an invariant, unique quantity, which can be physically measurable.

Assigned gauge enters in Feynman’s wavefunction adjusted according to the action-gauge principle rendering it non-unique. However, the methods of Feynman’s path-integral formulation determine a unique wavefunction for all values of the assigned gauge, which is the same as the quantum mechanical wavefunction determined by the earlier methods. Thus, the wavefunction defines an equivalence class, being the same for all values of the assigned gauge. Consequently, the wavefunction looses the information contained in the assigned gauge; furthermore, the concept of physical measurability cannot be applied to it. However, its complex conjugate is its natural Wheeler conjugate and a gauge invariant, unique quantity can be constructed by multiplying the two, which is equal to the Born probability density. Therefore, the concept of physical measurability can be applied to the Born density, but it suppresses the information that may be contained in the gauge factors, natural and assigned, both. It should be mentioned that some gauge factors do show up in the wavefunction calculated from the pertaining equations but the Born density suppresses them also. This renders the Born density incapable of yielding all physical effects. As will be discussed in other articles, the gauge factors, natural and assigned, both, produce physically measurable effects, which are determined by supplementary methods.

Concluding Remarks

Observations in the quintessential double slit experiment are discussed in this article in some detail indicating a complex nature of the behavior of physical entities and the consequent Feynman’s multiple path formulation of quantum mechanics, which is an improvement over the earlier basically an empirical formulation of quantum mechanics but it still incorporates the wave characteristics intertwined with the particle properties and thus, the issues pertaining to the wave-particle duality remain as puzzling as before. This formulation also accepts the postulate that Born’s rule yields the probability of finding a particle in a space-time region. Wheeler’s multiple path formulation on the background of the Weyl geometry, which does not change the formal structure of the multiple path formulation, does alter the picture by formulating mechanics in terms of the underlying geometry. Wheeler naturally incorporates the assigned gauge and the related quantities explicitly, which is of a crucial significance as it introduces an element of arbitrariness although it leads to a deduction of a rule parallel to the Born rule, even if from an intuitive argument.

Following the above formulations, a recently adopted novel approach to developing a theory of mechanics is discussed. This approach is based on the action-gauge principle obtained as an extension of the action principle yielding the corresponding law of particle motion differing from the classical one. This law together with Wheeler’s formulation is used to obtain an adjusted form of Feynman’s formulation of quantum mechanics and to deduce the Born rule in about the same way as Wheeler deduced a parallel rule. Since this formulation is based on purely particle picture of the physical entities, it alters the foundational structure of mechanics in a fundamental way. A striking feature of the modified law of the particle motion is that it succeeds in explaining the wave-like behavior of particles in motion when the associated action is of the order of Planck’s constant and classical particle-like behavior of the entities when the action is large; transiting from one to the other as the action changes; thus eliminating the menacing wave-particle duality from the foundational structure of mechanics. These and other related issues together with the double slit experiment will be revisited to discuss the observations not discussed here.

While in Feynman’s picture, a “particle” observed in a space-time region arrives from “everywhere” along “all trajectories,” in the formulation based on the action-gauge principle, the particle arrives from a randomly selected location out of all in space-time along a trajectory traveling, walking, in steps of randomly selected elementals. With reference to Einstein’s assertion, “Subtle is the Lord, but not malicious; God does not play dice with the World;” it appears that God does play dice with the World every step of the way.

Let us indulge in some musing: If a particle is spotted in a space-time region, we do not know, where it came from; so we assume that it came from everywhere in Feynman’s picture, and from somewhere out of everywhere in the action-gauge picture. Then we consider all possible origins of the particle one by one but we do not know how it came, i.e., which path it took; so we assume it took all paths in Feynman’s picture and one based on a series of random selections out of all in the action gauge picture. Wheeler’s formulation is not very explicit in this respect; nevertheless multiple trajectories are assigned to particle in motion. Now all we can do is to formulate mechanics in terms of some type of an aggregate, which has no unique meaning as it can be altered by changing the assigned gauge, i.e., the unit of measurement, and thus, is not physically measurable. So we conjure up a unique quantity, the probability density, which submits to the concept of physical measurability but does not contain all the physically observable information; neither does the aggregate by itself. The assigned gauge that an observer can assign essentially “at will,” contains physically measurable information, imparting the ability to alter the perception of the physical reality to the observer. Thus, it appears that our perception of physical reality is a subjective manifestation of our ignorance of it.

image (c) gettyimages.com