Introduction

Though the concept of working with reminders is not altogether new, I feel ‘Vinculum’ is one good tool that is not explained or used in our school or college mathematics, or even in our daily lives. Once we understand and start using it, I am sure we can do some very (apparently) tough calculations. It can also be used effectively in algebra as well.

In fact, one can change a long subtraction into addition; or a multiplication of large numbers to an operation with very small numbers like 1, 2, 3 or 4

Wikipedia gives an account of Vinculum as follows:

“A vinculum is a horizontal line used in mathematical notation for a specific purpose. It may be placed as an overline (or underline) over (or under) a mathematical expression to indicate that the expression is to be considered grouped together. Historically, vincula were extensively used to group items together, especially in written mathematics, but in modern mathematics this function has almost entirely been replaced by the use of parentheses. Today, however, the common usage of a vinculum to indicate the repetend of a repeating decimal is a significant exception and reflects the original usage.”

However, we can use Vinculum to indicate

    (a) shortfall of a given number with respect to another number (a Ten-multiple normally), or

    (b) Surplus over a given number over a negative number (which is also a Ten-multiple normally).

The advantage of this notation is that you can avoid using brackets for negative quantities.

Let me explain with examples:

(Caution: Depending upon the nearest 10 digit number you take, the appearance of a 3 digit number may look like a 4-digit number but its value will not change, as can be seen from examples 4 and 6)

Operations:

Vinculum works like a minus (-) sign.

1. Addition:

Ex. 7: We know, 89 + 98 = 187;

Using vinculum we can represent it as

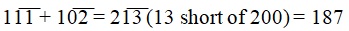
(Literally, we are only adding the differences of the given numbers with respect to a nearest 10 multiple, which are operationally small numbers, and then subtracting from the sum of the 10 multiples which is always easy.)

To get the difference with the nearest 10 multiple, we can use the following Sutra given by Swamy Bharati Tirtha in his book on Vedic Mathematics: All from 9 and the last from 10)

Ex.8: We know, 8979 + 9879 = 18858

Converting the numbers using vinculum,

 
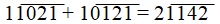
(1thousand 1 hundred 42 short of 20 thousand). Using the same sutra to convert it back, we get 18858.

2. Subtraction:

In fact, Vinculum comes in very handy in subtractions.  In fact, the whole operation of subtraction reduces to subtraction of only one number, and addition of the rest. How?

Let us see.

Ex. 9: Subtract 7768 from 11125

3. Multiplication:

4. Division:

This is equally applicable to division and makes division easy.  However, it is advised not to venture into it now, until a fair level of command of using Vinculum for the other three operations is obtained.

In the next article, we shall see how efficient vinculum operator is in finding out answers for large multiplications, finding squares, cubes etc.

Contiued to Next Page