Jan 01, 2026
Jan 01, 2026
by N. S. Murty
A New Method for ‘Finding the Cubes of Numbers’
The following method employs multiplication operations with small numbers like 1, 2, 3 and 4 to calculate the cube of any 2-digit number.
In the second stage, I also show how Vinculum can be used effectively to obtain the cube of any number.
I provide the operational steps with explanation in a tabular form:
For easy understanding I start with small numbers.
Ex1. To find the cube of 12
|
S. No. |
Operation |
Operation explained |
||||||||||||||||||||||||||||||
|
1 |
Take the nearest 10 as the base.
|
Base 10 |
||||||||||||||||||||||||||||||
|
2. |
Write the number 3 times one below the other.
|
|
||||||||||||||||||||||||||||||
|
3. |
Put the difference of the number and the base with sign to the right of each number with sign.
Product of the differences will be put in Unit’s Place of the final answer. (This is because we have taken 10 as base. If it is hundred, it will indicate Units and Tens place and so on depending upon the number of zeroes in the base) |
|
||||||||||||||||||||||||||||||
|
4 |
Multiply the three numbers with respective difference including sign and treat sum of the products as the value in Ten’s and Hundred’s place. (Note: Since 10 is the base no adjustments are necessary. When the base is different from 10, the procedure is explained later)
|
|
||||||||||||||||||||||||||||||
|
5 |
Place cube of the number to the left of zero in the base, in Thousand’s above place. (Note: If there is a carry forward in any place, effect the carry forward)
|
|
||||||||||||||||||||||||||||||
|
6 |
The value, after affecting the carry forwards if any, is the cube of the given umber. |
Ans. 1728 |
Ex. 2 Find the Cube of 14
|
|
10 |
(Difference between Number and Base with sign) |
|
|
|
|
|
|
14 |
+4 |
|
|
14 |
+4 |
|
|
14 |
+4 |
|
|
|
|
|
|
56 |
|
|
|
56 |
|
|
|
56 |
|
|
1 |
1/68 |
6/4 |
|
2 |
74 |
4 |
Note: 6 is carried over to Ten’s place and 1 is carried forward to Thousands.
Hence Cube of 14 is 2744.
Ex.3 Find the Cube of 24
The operation is the same as with base 20 or above up to 100 except the following.
Because there is no 20’s place in the decimal system, we multiply the sum of product of the number with its difference with sign with 2 when base is 20, (with 3 when the base is 30 and so on till base is 100). Any operations with respect to carry forwards will be taken up after the operation. The procedure is explained below, and the change is highlighted in bold:
|
|
Base: 20 |
(Difference between Number and Base with sign) |
|
|
|
|
|
|
24 |
+4 |
|
|
24 |
+4 |
|
|
24 |
+4 |
|
|
96 |
|
|
|
96 |
|
|
|
96 |
|
|
8 |
2/88 |
6/4 |
|
|
5/76 |
After multiplying (2/88) with 2 |
|
13 |
82 |
4 |
|
|
|
Ans. Cube of 24 is 13824 |
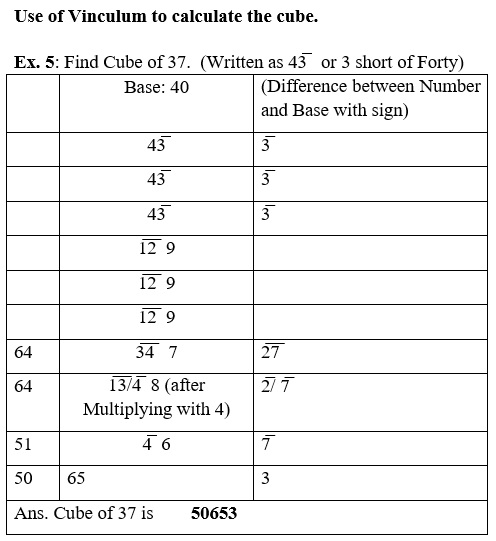
Ex.4: Find the cube of 38 using base 40 and 30
For comparison and easy understanding of the procedure, I show the sequence of operations with base 40 and 30
|
|
Base 40 |
(Difference between Number and Base with sign) |
Base 30 |
(Difference between Number and Base with sign) |
|
|
|
|
|
|
|
|
|
|
38 |
-2 |
|
38 |
+8 |
|
|
38 |
-2 |
|
38 |
+8 |
|
|
38 |
-2 |
|
38 |
+8 |
|
|
|
|
|
|
|
|
|
-76 |
|
|
304 |
|
|
|
-76 |
|
|
304 |
|
|
|
-76 |
|
|
304 |
|
|
64 |
-2/28 |
-8 |
27 |
912 |
51/2 |
|
64 |
-9/12 |
-8 |
27 |
27/36 |
51/2 |
|
The slash “ / ” separates the numbers to be carried forward to the left |
|||||
|
55 |
-12 |
-8 |
54 |
87 |
2 |
|
54 |
87 |
2 |
|
|
|
|
Ans. Cube of 38 is 54872 |
Ans. Cube of 38 is 54872 |
||||
It may be noted that using base 40 is easy since we have to manipulate with small numbers.

![]()
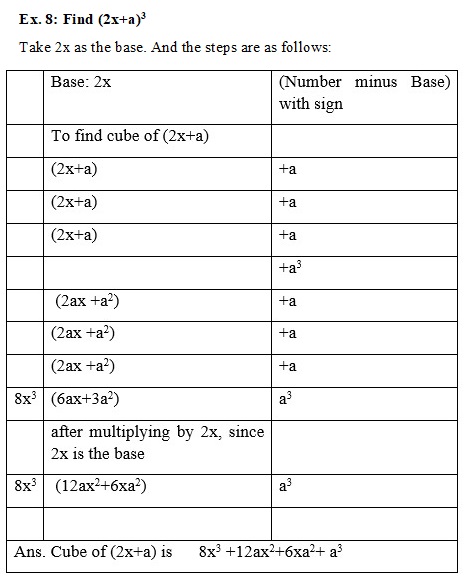
Take x as base and the working will be as follows:
(Note: In case of numbers the place values are automatically determined by the way we put the figures. But in algebraic expressions we have to signify them by appropriate powers. Hence, three times the sum of the multiplicand in step 2 is to be multiplied by the base instead of the coefficient of x alone)

14-Nov-2020
More by : N. S. Murty

|
Cube style is awsome |