Quantum Theories – Anomalies

Through every rift of discovery some seeming anomaly drops out of darkness
and falls as golden link into the great chain of order.
– Edwin Hubbel Chaplin

Quantum mechanics was formulated to accommodate certain observations that were at variance with the classical expectations. Observations in the double slit experiment were about the most intriguing ones, which delineated peculiar behavior of the entities observed, which was interpreted to be due to their dual nature, wave and particle. These observations were described in some detail in the article, “Perceptions of physical reality - 7.” In turn, quantum mechanics predicted some phenomena that were unexpected in the classical thinking. Almost all of such predictions have been confirmed experimentally, but they present some quite unsettling conceptual issues; major ones are discussed in the present article. As for the “chain of order,” thinkers search forever.

Passage around Hole in Space

If there is seeing without perceiving, there is also perceiving without seeing. If Ruby B were invisible we could infer her presence from your anomalous wobbling. Brown dwarfs and black holes, though hidden from sight, can be inferred from the anomalies they cause in their seeable neighbors. – Amy Leach in Things that are

As discussed in the article, “Perceptions of physical reality - 4,” electromagnetic potentials were introduced as mathematical auxiliaries to streamline the classical formulation of electromagnetism. Although the fields were deduced from the potentials and thus, they acquired mathematically secondary position, electromagnetism was still considered to be described adequately and completely by the fields. This changed after Aharonov and Bohm noticed, in 1959, that the quantum mechanics predicted some electromagnetic phenomena, which could not be adequately described in terms of the fields and concluded that the potentials have a physical significance.

Aharonov and Bohm envisioned some experiments illustrating the significance of electromagnetic potentials. One of them was realized by Chambers a year later, in 1960. Chamber’s arrangement is shown in Figure 1: S is a source of the electrons, which were collimated to be reflected at A and B to meet again on an observation screen. There is a thin long solenoid perpendicular to the plane of the figure based on the circle carrying an electric current, which produces a magnetic field enclosed by the beams SAX and SBX, where X is an arbitrary point on the observation screen.

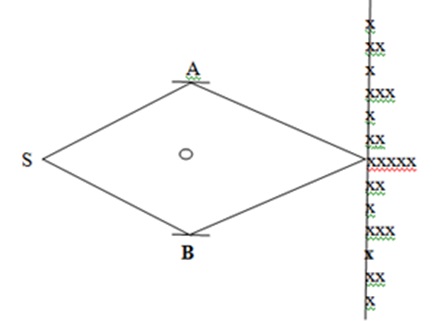
Figure 1. Aharonov-Bohm experiment

In Figure 1, the beams shown are classical, piecewise straight line paths. As discussed in the article, “Perceptions of physical reality - 7,” an electron has multitude of trajectories available to it, which although not classical, are concentrated about the classical ones. The Aharonov-Bohm argument is applicable to arbitrary trajectories. Since the cylinder is long and the experiment is conducted near one of its ends, it mimics a point magnetic monopole, enclosed by the beams. While the field is enclosed by the trajectories SAX and SBX, they do not pass through it. Extra care is taken in shielding the beams from the field. Geometrically, the field punctures a hole in space, i.e., a closed curve encircling the hole and remaining outside it cannot be shrunk to a point. In comparison, a closed curve in the complement of the hole and not enclosing it can be shrunk to a point.

This is essentially the same arrangement as in the double slit experiment except for the enclosed field. In this experiment also, an interference-like electron density pattern is observed on the observation screen for a fixed field; electrons on the observation screen are marked by x. As the field is varied, which is done by varying the current in solenoid, the density pattern shifts repeating itself periodically with respect to the enclosed field. Thus, the electrons carry the information about the field even though they never pass through it. This effect parallels the following scenario: Imagine two identical cows entering a thick forest who wander off grazing in different directions to meet again on the other side of the forest. There is a pond hidden inside the forest, which the cows have no way to see but their paths encircle it. Classically, there would be no way to know anything about the pond. However, quantum mechanically, the cows would have some sign, e.g., being wet, that would tell that the cows have passed through the water.

Quantum mechanics predicted this phenomenon, known as the Aharonov-Bohm effect, and Chambers confirmed it, but so ingrained was the concept in the minds of physicists that electromagnetism is described by the fields that Chambers’ and other experiments observing the effect were looked upon with suspicion and considered inconclusive. Finally Tonomura and coworkers confirmed the effect in 1986 with sufficient precision that left no doubt about its existence.

In fact, the potentials are not what affect the behavior of electrons in the above phenomenon; instead, this behavior is described in terms of the phase factors. The wavefunctions for the electrons along the two paths are related by a gauge transformation, which is equivalent to the wavefunctions differing from each other by a multiplicative phase factor. Two waves meeting in different phases show interference effect, which explains the above behavior, assuming the validity of the wave-particle duality. Although, the field is confined to a narrow region, the potentials and thus the phase factors are defined everywhere. Wu and Yang pointed out that electromagnetism is under-described by the fields and over-described by the potentials; it is adequately and completely described by the phase factors, i.e., the gauge transformations.

Since the two wavefunctions differ by a phase, Born’s probability density, being the square of the absolute value of wavefunction, corresponding to the two beams is the same. Thus the Aharonov-Bohm effect shows also the inadequacy of the probability density in describing the physical reality completely. The wavefunction by itself is also inadequate to describe it. Instead, it is the gauge transformation, a geometrical concept; that together with the wavefunction describes physical reality adequately. This constitutes yet another link in the chain of the perceptions of physical reality in geometrical terms.

Passage through Barrier

Consider a beam of particles travelling from left to right that encounters a potential barrier as shown in Figure 2. Classically, if the potential strength is more than the energy of each individual particle, the particles would be reflected; if it is less, then they would pass through the barrier. Quantum mechanics predicts that in both cases, in fact in all cases, some particles would be reflected and some would be transmitted; difference would only be in the fractions transmitted and reflected.

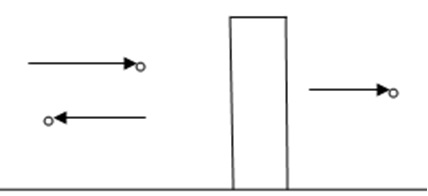
Figure 2. Potential barrier

Again, one can imagine a parallel scenario: A hunter is chasing a cat; the cat finds a wall thick enough that the energy of the bullets is not sufficient to penetrate it classically; and hides behind the wall. The hunter cannot jump over the wall like the cat but keeps firing. Quantum mechanically, some bullets would pass through the wall to strike the cat. This effect is called the tunneling effect, which has been exploited in some major technological advances. Tunneling can also be understood in terms of a wave phenomenon.

Entanglement

In an attempt to show incompleteness of quantum mechanics, Einstein, Podolsky and Rosen (EPR) in 1935 devised a thought experiment. To avoid technicalities, the basic argument is illustrated below with a concrete example.

Consider a system in spin zero state, e.g., a pion, which disintegrates in two subsystems, electron-positron pair. In Figure 3, the pion at X disintegrates in two particles, A and B, one of them being an electron and the other, positron. The component of spin of an electron along one axis, say x-axis, can have two values, half and negative half, termed spin up and spin down; same is the case with positron. In a measurement of the spin of one particle, probabilities of the result being spin up and down are equal. Spin is a conserved quantity. Therefore, if the spin of electron along x-axis is measured to be up, the spin of positron in x direction must be down, since the total spin, that of the composite system pion, is equal to zero; and thus the electron-positron pair is entangled.

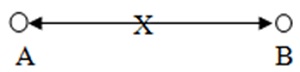
Figure 3. Entangled particles

A measurement can be carried out on one of the particles when the particles are separated by so large a distance that the measurement can be carried out in lesser time than light would take to travel from one particle to the other; i.e., there is no impact of this measurement on the other. According to special relativity, no signal, information, can travel faster than light. According to the EPR argument, one can determine the spin of positron along x-axis by a single measurement of the electron spin without in any way disturbing the positron. Therefore, the positron spin along x-axis must have had that value all along, i.e., it is physically real. Similarly, the spins along y, z- axes must be real. Since quantum mechanics cannot determine the spin values, a physically real observable, quantum mechanics is incomplete and fundamentally inadequate.

Now, according to the uncertainty principle, the spin along x-axis and along any other axis cannot be determined with certainty simultaneously as is the case with the momentum-position pair. However, the spin along one direction can be determined exactly if that in the other directions is left completely undetermined. Thus, an exact determination of the spin of electron along x-axis renders its spin along say, y-axis completely undetermined. But one can measure the spin of positron along y-axis, and by the conservation property, determine that of the electron and thus can determine the spin of electron exactly along x as well as y direction simultaneously violating the uncertainty principle.

In their original treatment, EPR considered momentum and position instead of the spin. Momentum of the EPR composite system and thus, of the pair of particles, is equal to zero; and the relative distance of the two particles is a non-zero constant; both of these are conserved quantities, entangling the particles. Relevant properties of the EPR particles and the spin properties of the system considered here are the same: According to the uncertainty principle, the momentum and position of a particle cannot be measured with complete precision simultaneously, but one of them can be with complete precision if the other one is left completely undetermined. In the example cited above, the spins in different directions cannot be measured with certainty simultaneously, but in one direction it can be determined with certainty if the other one is left completely undetermined. Now the argument can be transposed exactly from the above case to the momentum-position pair of observables, to show that they are both physically real, which quantum mechanics cannot determine and each one can be determined experimentally exactly simultaneously violating the uncertainty principle.

The argument of EPR is based on the assumption that no signal, information, from one particle to the other can travel faster than light, as dictated by the special relativity. Alternatively, if some nonlocal effects exist in nature, then this argument is invalid, but non-locality, equivalently action at a distance, was unacceptable to these authors. However, existence of nonlocal effects in nature has been experimentally verified validating the pertaining quantum rules of calculations predicting the experimental outcomes. Initially, there were some technical difficulties with this verification with the momentum-position pair, i.e., with the original EPR system. For the spin observable, the verification was found to be easier, which was done. Since then the original EPR experiment has also been realized confirming the existence of non-local effects.

As an alternative to non-locality, it has been suggested that each particle carries the information coded in it at the time of disintegration, i.e., remembers its history; which would transfer the entanglement to the code rendering them independent but different from its bare form; i.e., the particle together with the coded information defines it in its completeness at the moment of disintegration. However, one would not know the coded information without measurement.

EPR argument was described to be the “bolt out of the blue,” when it was presented initially. Confirmation of the non-local effects was done after Einstein’s death. It was said then that “Einstein must be turning in his grave,” at verifications of existence of non-local effects. In any case, the entanglement phenomenon presents some puzzling situations, e.g., a measurement on one of the partners in an entangled system at any time anywhere in the universe would impact upon the other partner.

Schrödinger’s Cat

Furthering the discussion about the EPR argument, Schrödinger devised another thought experiment, also in 1935. In this arrangement, a cat is encased in a chamber as shown in the top Figure 4, with some radioactive material and a flask containing poisonous gas. There is also a mechanism that triggers a hammer breaking the flask releasing the gas and killing the cat as a particle is emitted from the radioactive material. The matter to decide is whether the cat is alive or dead at a given time.

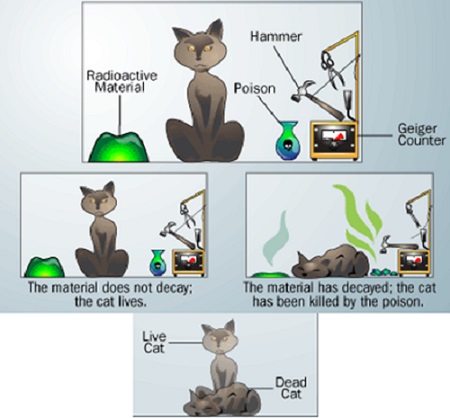
Figure 4. Schrödinger’s cat

As illustrated in Figure 4, if the radioactive material has not decayed yet, i.e., has not released a particle, the cat must be alive; if it has decayed, then the cat must be dead. However, from the quantum mechanical rules, one can only compute the wavefunction representing the state of system, which is a superposition of “pure” states. The wavefunction can be used to calculate the probability of emission of a particle in certain time and thus, of the cat being alive after that much time, yielding also the probability of the cat being dead, both between zero and one. But if one looks into the chamber, which can be assumed to have a glass window, the cat would be found either dead or alive, not both.

Quantum mechanically, each measurement yields a definite outcome, but with a probability attached to it. However, after the measurement, the system is in a definite state as is the case with the cat and with the EPR system. But this definite state is not discernible from the quantum mechanical calculations; it requires a measurement. Until somebody looks at the cat, it is in a superposition of states, both dead and alive; in a suspended state of animation; upon observation, it is in a definite state, either dead or alive, not both. Cat in superposed state is mimicked in the bottom Figure 4.

Question arises whether an act of observation determines the state of system it was already in or it forces the system to acquire the state observed from a superposition of states. While there is no conclusive evidence yet and the systems as large as a cat have not been constructed in superposed states, systems on the atomic scale, e.g., the photons, in superposed states are alleged to have been constructed.

Observations made by human observers are always at macroscopic scale and inferences about the microscopic systems are drawn from the macroscopic data. There is a troublesome lack of clarity about how the microscopic system is coupled, quantum mechanically, with the macroscopic, which is quite succinctly exemplified by the Schrödinger cat experiment.

Concluding Remarks

While the first two examples described above, passage around a hole and through a barrier, are counter-intuitive in the framework of the classical thinking, they do not pose any “paradoxical” situations except the wave-particle duality, which is the fundamental premise of quantum mechanics. Once the wave-particle duality and the resulting formalism of quantum mechanics are accepted, these effects are successfully described.

The other two effects question the “validity” of quantum mechanics together with its fundamental formulation. Basic issues here are whether an objective reality exists or the only reality there is, is what is observed, perceived. The EPR argument purports that it does exist and since quantum mechanics is incapable of describing the “reality,” it is incomplete and fundamentally inadequate. The argument also questions the limitations on the measurements set out by quantum mechanics arguing that the “objective reality” can be determined precisely by observations. The Schrödinger’s cat argument adds to the EPR argument.

Underlying the paradoxical situation is the premise of quantum mechanical formulation that a physical system is in a superposition of states but it is found in a single pure state upon measurement e.g., Schrödinger’s cat is, exists, in a superposed state of two states: Being alive and Being dead; until it is looked upon; but after the observation it is, exists, only in one of these states.

There are several “interpretations” of quantum mechanics and supplementing arguments that address these issues, which will be the topic of the next article in this series.