Quantum Theories – Interpretations

Although the metaphysical element underlies all basic physical theories and interpretations are required for their basic understanding as well as to relate them with the observations, in classical mechanics there was little room to address observations that were considered anomalous. On the other hand, quantum mechanics has tried and continues to try to come to terms with many such observations, some of which are discussed in the article, “Perceptions of physical reality – 8,” referred to here as [8 ]. Interpretations of quantum mechanics were developed to address the pertaining issues.

Founding principles of quantum mechanics were developed during the early twentieth century in an effort to reconcile the wave-particle duality that was the main outcome of observations in the quintessential double slit experiment discussed in detail in the article, “Perceptions of physical reality – 7” referred to as [7 ] here. The doctrine of duality itself continued to be one of the major concerns in developing the interpretations, which were needed also to understand the physical and epistemological contents of the empirically deduced postulates that incorporate this duality. The rules of calculations based on the postulates have proven to be immensely successful in describing physical phenomena. It has been said; referring to these rules; that early twentieth century was the period when second rate scientists developed first rate physics. However, interpretations of quantum mechanics still remain unsatisfactory, to the extent that they render the success of the rules of calculations rather irritating. Interpretations themselves have been interpreted with differing views; some of them even involve the mind.

Major difficulties the interpretations endeavor to address are the wave-particle duality, apparent role of observers in the measurements, and the phenomena associated with entanglement, all of which are related to each other; in fact, they are all essentially equivalent. Here we describe the major interpretations briefly.

Copenhagen Interpretation

In quantum mechanics, state of a physical system is represented by its wavefunction, which can be expressed as a superposition of many “pure states.” Outcome of a single measurement shows the system in one of the pure states. The Copenhagen interpretation, due mainly to Bohr and Heisenberg, was the first attempt to understand this state of affairs, which “explains” it by assuming that the wavefunction “collapses” into a definite state by an act of observation. This “explanation” means that quantum mechanics describes the system as a collection of many possible outcomes; an observation reveals one of them depending upon the method of observation. Thus, “reality” is determined by the act of observation; therefore it is subjective, not objective.

Copenhagen interpretation’s response to observations in the double slit experiment is that an entity has no “form” until observed; it acquires a form upon measurement. However, if the experiment is designed to observe a particle, one observes it as a particle; if it is designed to observe a wave, the entity is observed as a wave: If one registers individual entities or collects the entities, it is observed as a particle; if one collects large number of entities from both slits, it registers its wave nature. However, individual entities are always observed as particles; thus the wavefunction should have collapsed; yet an interference-like pattern emerges after many have arrived; the question remains if the entity had a waveform before an interference-like pattern emerges, even though each one was observed as a particle. Attempts to observe individual entities as particles while retaining its waveform have failed and continue to fail.

As indicated above, if one knows “which path” the entity took, it is identified as a particle; if “which path” information is not available, it is identified as a wave. In the double slit experiment, data collected separately from individual slits and then superposed shows the entities behaving as particles; if one collects the data from both slits, they behave as waves. However, there are essentially double slit experiments where one collects data in one single experiment and separates it in two or more sets of data, each containing “which path” information; thus identifying each entity as a particle; and conclude that the wavefunction has collapsed. But, one can combine two certain subsets of data in a way that “which path” information is not available from the combined set; it is erased, which reveals the wave nature of the entity. This process is termed the “quantum eraser:” Thus, a collapsed wavefunction can be de-collapsed. Several experiments posing such puzzling situations are described in: J. Horgan, Quantum philosophy, Scientific American, 1992 July issue, pp. 94-104.

Subjectivity of reality is extended further in responding to the EPR objection. Consider the experiment when spin is measured. It is asserted that the observer who determines the spin of one particle knows the spin of the entangled, other particle, but the “observer” at the location of the other particle does not; information that “observer” can be conveyed by the first, which cannot travel faster than the speed of light. Omitting some intricate points, an implication of this situation can be pointed out: Even the “collapse as well as de-collapsing” of wavefunction” and the wavefunction itself are subjective; even the wavefunction is not “real.”

The cat phenomenon resembles the double slit experiment with one slit open: Radioactive material is bulk material as is the source in the double slit system; in both cases the radiation of the entity is a bulk stochastic, semi-classical, random process; and the entity is captured by the triggering mechanism just as by the detector. Thus, in case of the cat consider the wavefunction of the entity after its radiation. Bohr argued that as a particle is registered by the triggering mechanism, the Geiger counter, the wavefunction has collapsed as in case of the double slit observation. Based on this argument, Bohr did not consider the cat phenomenon a paradox.

Other arguments consider the sequence of events that follow assigning a wavefunction to the cat, although its definition is not clear. The wavefunction before any observation describes the cat in a suspended state of animation, both dead and alive, which is paradoxical. If the wavefunction of the cat collapses at the first observation, the situation is not all that different from when a scientist has left the lab leaving an assistant to make observations in the double slit system. It is still not clear when the cat dies, before an observation is made or after. Various arguments persist as to when the wavefunction collapses, cat dies, which is clearly indicative of lack of clarity.

Schrödinger is known to comment on this state of affairs that he regretted ever having met this cat; he also expressed regret at having anything to do with quantum mechanics even though his equation was the first one and most omnipresent among the quantum mechanical equations describing the physical systems.

Passage around a hole in space and through a barrier; pose no further problem with this view: Quantum mechanics is a nonlocal theory, which invalidates the EPR argument; and the wave nature allows the entity to pass through a classically impenetrable barrier.

Most physicists accept the Copenhagen interpretation even though it has been said that to accept it is to accept meaninglessness. In the Copenhagen view, the wavefunction together with the equations governing its evolution are basic and sufficient to the understanding of and for describing a physical system and thus, no further analysis is really necessary. Heisenberg and Born, paper delivered to Solvay Congress of 1927, summarizes this view:

We regard quantum mechanics as a complete theory for which the fundamental physical and mathematical hypotheses are no longer susceptible of modification.

This is “justification” by declaration. Some consider the questions asked meaningless, e.g., Feshbach has commented, “Ask a silly question, get a silly answer,” i.e., asking such questions is illegitimate, paradoxical situations with quantum mechanics are not. This attitude is further reflected in a phrase attributed to David Mermin of Cornell: Shut up and calculate. Supporters of the Copenhagen interpretation subscribe to this view.

In view of the above, it is difficult to consider quantum mechanics together with the Copenhagen interpretation even a second rate physics; let alone first rate. That is one reason why efforts at developing more palatable interpretations have continued and some alternatives have been developed; main ones are discussed below.

Pilot Waves

The pilot wave interpretation of quantum mechanics adopts the view that a particle follows a definite trajectory but guided by a wave, and the trajectory remains unknown. While the idea had been suggested earlier, mainly by de Broglie, it was developed by David Bohm in the mid 1950s. The picture that emerges is that of the probability density flowing as a classical fluid of a properly defined velocity coupled with a classical particle in a potential field defined by its quantum mechanical wavefunction. This potential, called the quantum potential or the Bohm field, differs from the classical potential by a pathologically small term, but it impacts upon the particle trajectories in a fundamental way. The Bohm trajectories in the double slit experiment are depicted in Figure 1.

Figure 1. Bohm trajectories in double slit experiment
(Image - Courtesy Wikipedia)

Since the trajectory a “particle” follows is not known, the “particle trajectories” are the hidden variables in this formulation. For this reason, Bohm’s formulation is considered a hidden variable theory. There are other hidden variable theories not considered here. It is anticipated that the hidden variables of such theories will become known in a better theory than quantum mechanics, but given the nature of observations it is also thought that there may never be such a theory. Some consider hidden variable theories justified.

In the Copenhagen interpretation, wavefunction is fundamental; particle has no meaning; it is just something resulting from the wavefunction collapse.Bohmian mechanics interprets the system as a particle following a trajectory guided by the Bohm field or a pilot wave, “probability wave,” not a physical wave. This “wave” flows as a classical fluid, i.e., a particle “floats” in a wave, moving as the wave directs it; the wave enables one to calculate the probability of the particle being in a given spacetime region. In a double slit experiment, probability wave view is that the wave passes through both slits but the particle passes through one; it is just that which one it passes through is determined by the wave, and it cannot be determined, which one.

In the pilot wave theory, although the doctrine of wave-particle duality is not directly accepted, it is nevertheless incorporated in it: Model has both, wave and particle interacting with each other; each one of the two can be invoked as needed. Also, the Bohm mechanics is a non-local theory as is the original formulation of quantum mechanics. Thus, the EPR argument is invalidated. In case of Schrödinger’s cat, it is a particle that triggers the hammer breaking the vial killing the cat, if it is found dead, but there is still a probability attached to it and one cannot determine from the theory what state the cat is in. Thus, not much is gained in terms of clarification.

Jean-Pierre Vigier, the foremost intellectual progeny of de Broglie and Bohm, described the basic content of the Bohm mechanics as follows: A particle in motion is like a twig floating in a river; in the double slit experiment, the river flows through both slits but the particle goes through one of them. This comment was made in a personal discussion after my presentation at a conference. I commented that use of the phrases such as “… is like …,” is “dangerous” in a serious scientific discourse for it is often used to camouflage the inadequacy of the respective concepts. The story of our disagreement took a life of its own in time, generating a heated exchange between the participants a couple of years later in another conference, which itself is indicative of a controversial nature of this theory.

Proponents of the theory assert that it provides a clearer picture of the quantum mechanical behavior, particularly as it describes the particle motion in somewhat classical terms and avoids the troublesome concept of wavefunction collapse, e.g., in the double slit experiment a detector detects a particle that exists even though the wave determines where it is detected. On the other hand, this theory takes the wavefunction to be fundamental, “physically real,” that determines the Bohm field, i.e., the Bohm field is defined in terms of the state of the system; it is not universal as are usual fields. Thus it is essentially equivalent to quantum mechanics and the Bohm field is as problematic as the wavefunction for the probability waves are not physical waves as waves are normally understood; it is just an abstract mathematical concept; just another way of presenting the quantum mechanical view. For the observations, the orthodox Copenhagen understanding introduces a new mechanism that of the wavefunction collapse that is not inherent in quantum mechanics, which Bohmian mechanics is considered to have avoided, but still quite tenuously: Collapsed and de-collapsed wavefunctions exist together as do wave and particle in the doctrine of wave-particle duality. For these reasons, this theory has not gained a strong foothold.

Many Worlds

Around 1957, Everett introduced the concept of relative states to eliminate the concept of wavefunction collapse, which was developed into what is commonly known as the many worlds interpretation, and developed further into many histories, and even many minds interpretations. This interpretation has enjoyed more popularity than the others at times, including the Copenhagen, although not always.

Consider a system being observed by an observing system, e.g., in the double slit experiment the system being observed is a “particle” by a particle detector represented by an observer state. Before the act of measurement is commenced, the two systems are independent; during the measurement, they interact with each other and after the measurement is completed, they are again in non-interactive state. Everett argued that for a complete understanding of the process, both systems should be considered as one composite system, i.e., represented by a single wavefunction. During the act of measurement, the composite system constituted of two interacting systems, evolves according to the rules of quantum mechanics. Thus, the act of measurement leaves both systems in different states than they were in before, called their respective relative states with respect to the state of the other; e.g., after a particle has been detected in one state, the detecting system is left in an observer state relative to the detected state. All possible outcomes of a measurement define such relative states, which are all necessary for complete description of the system. Thus, with each observation in a sequence, the observer state branches into different states, each one representing a possible outcome of the measurement, and after each sequence of observations, all branches exist simultaneously. Branching process is illustrated for the Schrödinger cat phenomenon in Figure 2.

Figure 2. Branching of states in Schrödinger’s cat experiment.
(Image - Courtesy Wikipedia)

In Figure 2, to the left the cat is both alive and dead before it is observed. The middle shows the effect of an observation when the cat branches off in two branches: In one of the branches, the radioactive material has decayed triggering the hammer breaking the vial containing poison killing the cat and in the other, the cat is alive. If an observer finds the cat dead (alive), it has entered the branch, the world, of the dead (alive) cat but the alive (dead) cat exists in another world inaccessible to this observer.

Subsequent to Everett’s original work, there have been number of adjustments, extensions and variations. Essential point remains the same that all possible outcomes of an observation exist simultaneously; each one somewhere, in some other “world,” unobservable to an observer in this “world.” Thus, in a double slit experiment with one photon at a time, the photon is assumed to interfere with other photons each one in another copy of the lab where the experiment is being conducted. In case of the EPR experiment with the spin measurements, if the spin is determined up in the lab, it is down in some other world. What an observer observes is what one measures. Other worlds where other possible outcomes exist are inaccessible to an observer in one world. With each subsequent measurement, this splitting or decoherence, which is a preferred term, takes place and the number of worlds increases, finally creating infinitely many worlds, in principle. “Many worlds” term has also been replaced with more palatable phrase “many histories.” Also, it has been anticipated that there may be some interaction between different worlds, and thus, decoherence, inaccessibility, may not be exactly valid, but this issue has not yet been conclusively settled.

Major objections to the many worlds interpretation are the existence of infinitely many non-communicating universes and there is no experiment that could determine their existence; the theory is untestable; therefore unfalsifiable. Cited advantages are replacing the concept of wavefunction collapse by decoherence making it a “deterministic, local and axiomatically more streamlined;” although critics question these claims. Further, precise understanding of decoherence is asserted to be lacking.

Proponents of the many worlds view consider the introduction of particles in the Bohmian mechanics unnecessary, since there exists a minimal assumption theory, namely, the relative state formulation that assumes only the wave nature. They also consider the Bohm mechanics essentially a many worlds theory, the worlds’ being the Bohm trajectories. As many worlds view, Bohmian mechanics is also untestable, implying unfasifiability.

None of the above interpretations has been universally accepted. This is the case also with the other interpretations that are not discussed here. Quite often the same properties of an interpretation are cited by the proponents and opponents as favoring their positions.

Once, one hundred scientists published a critique of the theory of relativity arguing that it was a wrong theory. Einstein responded: If I were wrong, one would have been enough. Similar situation exists here: If there were a scientifically tenable interpretation, one would have been enough. Since controversy persists about all the interpretations and they compete for popularity, none of them can be considered correct.

Gauge Description of Anomalies

Formulation of quantum mechanics based on the action gauge principle in terms of gauge transformations of the Weyl geometry was described in [7]. The founding assumption of the Weyl geometry is that the length of a vector at B transported along a trajectory from A to B is in general, different from that at A, with lengths at two points related by a gauge transformation, termed the natural or essential gauge. In addition, a measure of length, a gauge, can be assigned to the points, which is called the assigned gauge. Understanding of the quantum anomalies discussed in [8] as well as the double slit phenomenon, is described below in some detail referring specifically to each one of them on the background of this formulation. The description is based on the properties of the physical trajectories discussed in [7].

According to the Action-Gauge Principle: A particle follows a physical trajectory, i.e., the length of a vector attached to the particle resumes its original value at the terminal point of this path with classical action being the generator of change. Physical trajectories depend on the assigned gauge, which is the same for physically equivalent points; otherwise not. If the assigned gauges are identical at the initial and the terminal points of a trajectory, then they nullify each other; also if a trajectory is a continuing union of two paths, then the value of the assigned gauge at their common point also becomes ineffective. The values of such ineffective gauges can be taken to be unity. It should be understood that for a trajectory to be a continuing union of two paths, the terminal point of one path should be the same geometrically, and physically equivalent, to the initial point of the other.

Smallest monotonic physical trajectory is called an elemental path. A monotonic physical trajectory is a continuing union of the elementals; trajectories of macroscopic dimensions are concentrated about the classical trajectories regardless of the assigned gauge; and the trajectories of microscopic dimensions possess wave-like coherence, which arises out of the fact that a physical trajectory constitutes of randomly selected elementals. This covers the monotonic trajectories. Non-monotonic trajectories will be considered below as encountered.

In addition to altering the conceptual structure of quantum mechanics, this formulation adjusts its formalism also in a significant way by introducing the assigned gauge altering the meaning of wavefunction. As its consequence, a wavefunction represents a class in that it is the same for all values of the assigned gauge; i.e., it is gauge neutral. In fact the assigned gauge is absorbed in the wavefunction and thus, the representative wavefunction is the same as for unit gauge.

Double Slit Phenomenon

Consider the double slit arrangement of Figure 3 below, which is the same as Figure 1 of [7]:

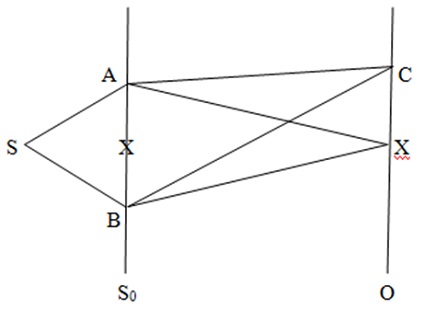
Figure 3. Double slit system with equivalent A and B

In Figure 3, S is the source, A and B are the slits in the screen S₀, C is an arbitrary observation point on the observation screen O and X marks the central point. The trajectories shown are the straight lines although all trajectories joining the respective points are possible for a particle to take.

Assignment of gauges can be somewhat intricate at times, which is described here for this case that explains the concept for other cases as well. Particles reaching about C along AC and BC experience the same interaction with the detector at C implying that the assigned gauge is the same about C as the terminal point of AC and of BC. The system of AC and BC is geometrically equivalent to the continuing union of trajectories from A to C and from C to B, constituting a single non-monotonic trajectory with the action increasing from A to C and decreasing from C to B. If a particle incident along AC was reflected about C along CB, the assigned gauge at C as the terminal point of AC and as the initial point of CB would still be the same but the trajectory ACB would be monotonic. In both cases, C is common to the corresponding constituent trajectories and thus, the gauge at C is rendered ineffective.

Radiation process is a classically stochastic bulk activity as is the interaction with a detector, both represented by the assigned gauge. By the above argument, the gauge at S is ineffective. Let S be centrally located and the slits be identical. The beams SA and SB are reflected about A and B respectively. As above, the gauges about A and B would also be ineffective. Now, let an inequivalence between the slits be introduced on the right side. In case of the electrons, this can be done, e.g., by scattering the photons from the beam behind but close to slit A. In this case, the gauge about A as the terminal point of SA would be different from that about A as the initial point of AC. However, the gauges about A and B as terminal points of SA and SB, respectively, are identical, which are the end points of the non-monotonic trajectory ASB, rendering them ineffective. Also, the action along ASB is zero. This renders the configuration left of the slits inconsequential, which will be ignored for convenience. With this, the gauges at A and B differ from one. A system can be considered with or without such decomposition for convenience without affecting the result of analysis including the cases that parallel this system with A and B equivalent.

If a net assigned gauge is introduced about a point A’ away from a slit, A, along AC, the configuration left of A’ and the corresponding point along BC can be ignore by the above argument. In cases of confusion whether a point of intrusion is common to the corresponding constituents, one can compare the effect of the complete gauge transformation. For example, in the present example with intrusion about A’, one can calculate the complete gauge transformation with or without intrusion. If they are different, a net assigned gauge has been introduced at A; otherwise not. With this clarification, we return to the consideration of the double slit phenomenon for A and B being equivalent to each other and not equivalent.

First consider the case when the slits A and B are physically equivalent and thus the assigned gauges there are equal. Since A and B in this configuration are the end points of a single, non-monotonic, trajectory ASB with equal assigned gauges, the assigned gauges there become ineffective and thus, can be set equal to one as everywhere else.

Let the constituent trajectories AC and BC be straight lines, i.e., the classical particle trajectories. The action along the trajectory from A to C to B is the action along the trajectory from A to C minus the action along the trajectory from B to C. If this action is an integral multiple of the action along an elemental, the length at B of a vector transported from A to C to B is equal to that at A. For non-zero integral multiplier, this can be seen from the definition of an elemental: A vector transported along an elemental has the same length at its end points. For the multiplier being equal to zero, i.e., if C is located at X; the action along the configuration is equal to zero; thus the corresponding gauge transformation being the exponential of a constant multiple of the action, is equal to one, implying the same. In fact, the configuration from A to X to B is equivalent to a point, which is the trivial monotonic “trajectory;” nevertheless it is allowed; and while it is of no significance for the monotonic physical trajectories, it is significant in case of non-monotonic trajectories as discussed here. For C at locations other than X, this configuration is effectively equivalent to a monotonic trajectory constituted of the continuing union of elementals. Thus, this configuration constitutes a physical trajectory for all locations satisfying the stated condition and hence, allowed for a particle. This is an example where two macroscopic trajectories combine to yield an effective microscopic trajectory.

Since the trajectories from A to C and from C to B are classical, the action along the trajectories in their neighborhoods differs by a small amount implying the existence of an abundance of physical trajectories in a close neighborhood of the piecewise classical physical trajectory from A to C to B, yielding a high density of particles after many have landed on O; and in between the high density regions, there are low density regions by similar argument. This is the same argument as used for the monotonic physical trajectories in [7]. Since there is a random selection of elementals at each step, a particle can land anywhere on the screen. However, this location is not completely random as the wave-like coherence is built into the microscopic steps, which becomes significant in case of microscopic trajectories; and this configuration is effectively a microscopic trajectory.

Now consider the case when the slits at A and B are not physically equivalent, which can be for various reasons. The case of the inequivalence caused by an intrusive observation discussed above is considered further here for clarity; essential argument is the same in all cases causing such inequivalence. This requires some intricate mathematical estimates; results are stated avoiding the technicalities. As indicated above, an intrusive observation can be made in an experiment conducted with electrons by scattering photons behind S₀ close to A as shown in Figure 4, to see if there is an electron coming out of A. Figure 4 is the form of Figure 3 resulting from the intrusion except that scattering of photons is indicated by the arrows, which would shift the beams AC to AC’ for all locations of C including X, by transferring some momentum from the scattered photon to an electron in the scattering region. If an intrusion is made away from A, it would be equivalent to assigning a gauge in the region of intrusion, which can be analyzed in a similar manner.

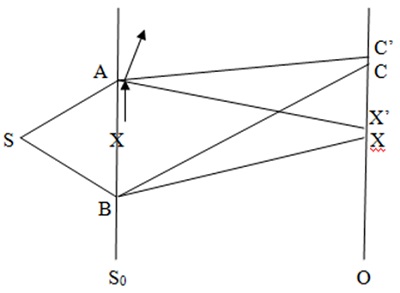
Figure 4. Double slit system with ineqivalent A and B

For low energy, i.e., low frequency photons, the transferred momentum is small causing a small shift of C, for which there are still many correlated trajectories constituting composite non-monotonic physical trajectories AC”B, where C” represents the terminal point of the trajectory in a small neighborhood of AC, AC’ on O. This applies to the configuration for all locations of C including X. This causes the density pattern to shift and blur. As the frequency of photons is increased, the transferred momentum increases increasing the shift and blur of the density pattern. When the shifted point reaches about the nearest minimum, there are hardly any correlated trajectories causing the interference-like pattern to about disappear. At this point, the trajectories AC” and BC” are uncorrelated and must be considered independent monotonic trajectories.

Monotonic physical trajectories of macroscopic dimension are concentrated about the classical particle trajectories, i.e., the ones yielded by the action principle, which in this case are AX” and BX; and the assigned gauges at A, X”, X and B are all different from one, which is inconsequential for the macroscopic almost classical trajectories. Thus, a classically expected behavior of particles would be observed, which also implies almost zero density away from X, X”.

The precision of the location of a particle, including photon, is the corresponding elemental. For photons of frequency low enough that the interference-like density pattern is discernible, the elemental is at least equal to the distance between the slits and thus, it cannot be determined which slit the electron passed through. For high frequency photon, when the slit which the electron passed through can be determined, the interference pattern disappears due to a large shift.

Now consider the observation when the electrons coming from A are collected. In this case the assigned gauges about A and the collection point are different and both are different from one. From the above discussion, it follows that classically expected behavior of electrons would be observed. All observations in double slit like experiments can be described in this manner.

From the above: An act of observation is an assignment of a gauge to points in the underlying manifold introducing additional structure to its geometry, and the perceived reality is determined by the system and the geometry that includes the alteration to it by the observer assigned gauge, indicating an impact of the observation on the perceived reality.

The reality that the wavefunction represents is a representative reality, which is the same for all assigned gauges. It is clear from the above discussion that the assigned gauges produce observable effects, which cannot be determined from the wavefunction. While the wavefunction is considered to represent the state of a system completely in other interpretations, one way or the other, in this formulation it is clearly not. Reality is defined uniquely with wavefunction coupled with the assigned gauge; both together define a unique reality; which is the perceived reality with respect to that particular gauge. The wavefunction suppresses the information contained in the assigned gauge; the probability density suppresses the information contained in the assigned as well as the essential gauge, which is clear from the Aharonov-Bohm-Chambers experiment.

Passage around Hole in Space

Chambers realization of the Aharonov-Bohm experiment is depicted in Figure 5, which is the same arrangement as of Figure 1 of [8], where the pertaining discussion is also available.

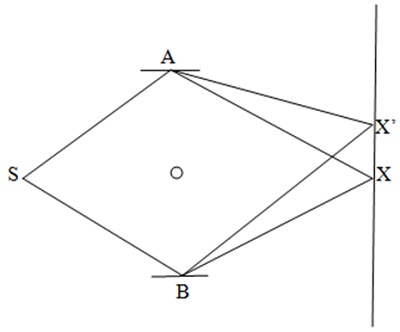
Figure 5. Aharonov-Bohm experiment

In Figure 5, S is the source of electrons, A and B are the reflectors, the enclosed magnetic flux is shown by the circle, X is the central location on the observation screen and X’ is an arbitrary observation point. Classically, the electrons travel along the straight lines: SAX(X’) and SBX(X’), which constitute a non-monotonic trajectory SAX(X’)BS. If this is a physical trajectory, all physical trajectories are concentrated about it. The assigned gauges at S, A, X(X’) and B are different from one, but they are effectively equal to one as each of these points is common to and physically equivalent for the pairs of two relevant pieces.

First consider the case with zero magnetic flux, which is essentially the same as the double slit experiment with the assigned gauge equivalent to one everywhere. While a part of the configuration was ignored in case of the double slit experiment, whole configuration is included here as it is more convenient. Assuming the arrangement of Figure 5 symmetric about the straight line joining S and X, there would be high density about X flanked by regions of low and high density, i.e., and interference-like pattern. The action along SAXBS, which is just the free particle action, is equal to zero.

For a non-zero flux, even if the paths of electrons are isolated from it, the electromagnetic potentials are non-zero everywhere, and for all cases, the flux, is equal to the electromagnetic potential integrated along SAX(X’)BS. Consequently, the essential gauge in general for this arrangement is the product of the free particle gauge and the exponential of a constant multiple of the flux. Thus, if the flux is altered from zero to a non-zero value, SAXBS is no longer a physical trajectory; instead, a shifted trajectory, e.g., SAX’BS would be physical, yielding a high density about X’. It is clear that this shifts the density pattern. As the essential gauge generated by the flux reaches the value equal to one, the arrangement becomes equivalent to the case of no flux, and hence, the original density distribution repeats itself periodically with respect to the flux. Thus, just the definition of the physical trajectories is sufficient to describe the Aharonov-Bohm effect successfully, a rather remarkable result.

Passage through Barrier

Figure 6, which is the same system as Figure 2 of [8], shows one-dimensional motion of a particle that encounters a potential barrier of finite extension. S is the source. Classically, the particle travels along SA encountering the barrier at A; if the strength of the potential is less than the energy of particle, it passes through traveling along AE; and if the strength is more than the energy, it is reflected along AF. AF is along AS; it is shown here separate for clarity.

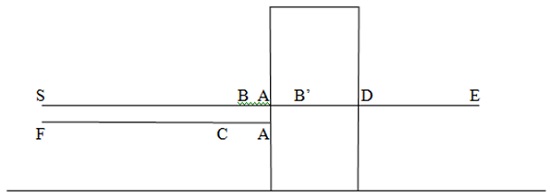
Figure 6. Potential barrier

Now consider the motion according to the action gauge principle taking the assigned gauges into account. Properties of this system are stated here omitting the technical details to indicate the basic argument. First consider the case when the potential strength is less than the particle energy and thus, classically, the particle would be transmitted. The action in this case increases along SAE, although the rate of increase is lower along AD. Thus, the trajectory SAE is monotonic. Since A and D are in the interior of a continuing trajectory with no imbalance in the gauge, assigned gauges there become ineffective and the gauges at S, E are inconsequential for the argument.

A physical trajectory is constituted of the elementals. Let AB be constituted of an integral number of elementals. There is a point B’ as shown such that the length at B’ of a vector transported along BB’ is the same as at B, and hence, particle can reach B’. By the same argument, the particle is transmitted at the other boundary. Physical trajectories are concentrated about the classical physical ones and they have a spread in terms of energy. Therefore some would have less energy than the potential, which would be reflected classically. Again, a point C exists such that the union BAC, which too is monotonic, is physical; implying the existence of the reflected physical trajectories about them. Thus both, transmission and reflection would be observed at A; and also at D by the same argument.

Now consider the case when the energy is less than the potential strength. In this case, the action increases from S to A and then decreases from A to D, increasing again from D to E. Thus, SADE is a non-monotonic trajectory with A and D being the inflection points. However, existence of a reflected C and transmitted B’ still follows from the same argument as above.

Entanglement

System of two entangled particles is shown in Figure 7, which is the same as Figure 3 of [8], where further details are available. Two particles, A and B, which are entangled though some conserved quantities, e.g., momentum and relative position, disintegrate at x and travel in opposite directions. EPR argument is that measurement of the momentum of A determines that of B without disturbing it; hence it must be “real;” but quantum mechanics cannot describe it. Also, position of B determines that of A. Thus both, the momentums and positions of both particles are determined exactly simultaneously. Since, the uncertainty principle prohibits this, it is violated. The argument is based on the assumption of locality.

Figure 7. Entangled particles

Since the theory being considered in the present section is non-local, as is clear from the above discussions, EPR argument is invalidated. Present formulation differs from the earlier one conceptually in that it is the trajectories that are entangled, instead of the particles, which in this case are Ax and Bx. Such trajectories can be considered a non-monotonic trajectory with the point of inflexion being the correlation point, common to the two monotonic segments. For the EPR system depicted in Figure 7, the trajectory AB is non-monotonic with the action decreasing from A to x and increasing from x to B. The assigned gauge at the inflection point x, which is fixed, is ineffective. This system is essentially the same as the double slit experiment except that there the point of inflexion changes due to interruption, while here it is fixed.

Let AB be a physical trajectory before a measurement is made. As discussed earlier, an act of observation is an assignment of a gauge. Thus, a measurement at A assigns a gauge at A; consequently, AB is no longer physical. A physical trajectory can be found in its neighborhood by adjusting the point B compensating for the assigned gauge at A. If a quantity is conserved, this adjustment would effectively maintain the conservation property. This shows the non-local nature of this theory even more clearly, which is the “reality.” As in case of the double slit experiment, correlated paths possess wave-like property, which can be uncovered by counting the number of particles arriving at different locations along the path when a large number of such experiments are conducted. A large intrusion also breaks up the correlation as the minor adjustments do not suffice after which each particle travels as a free particle.

Schrödinger’s Cat

Realistic depiction of Schrödinger’s thought experiment is given in Figure 4 of [8]; the corresponding essential schematic is given in Figure 8 below. In Figure 8, S is the radioactive material, T is the triggering mechanism, which releases the poison P to reach the cat C; the observer O observes the cat.

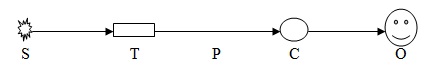
Figure 8. Schematic of Schrödinger’s cat experiment

Emission of a particle from S is essentially the same as the radiation from any other source, e.g., in the double slit experiment, which is modeled as stochastic processes. This part is in fact not essential element contributing to the “paradox.” In the present context, the emission activity is represented by an assigned gauge at S and the detection of particle by gauge at T. Triggering mechanism and release of poison, as well as its interaction with the cat are bulk activities; their details are not clear. The process can be represented by a trajectory from T to C with different assigned gauges at T and C. The assigned gauge at T as the terminal point of ST is different from that at T as the initial point of TC for the interactions are different. Then the observation process, e.g. photon from C to O, can be considered along a trajectory CO with different values of the assigned gauge at end points. The trajectories shown here are straight lines.

The “wavefunction of the cat” is identifiable with the wavefunction of the entity at C, which is the aggregate over all paths from S to C. This wavefunction has two observable states: Cat is either dead or alive. This is the same situation as with a spinor where spin can be either up or down, which cannot be determined without observation.

As discussed earlier, a wavefunction represents a class in that it is the same for all values of the net assigned gauge; the representative wavefunction is the same as for the unit gauge. Perceived reality is defined uniquely with wavefunction coupled with the gauge assigned by an observation. Before observation, the cat “is not” in a suspended state of animation; it is just that the representative wavefunction defines it in a state of suspended animation; and not just in a superposition of two states but of all possible observable states. In this case, the act of looking inside the box, an act of observation, assigns a gauge through a trajectory CO with gauges assigned at C and at O, e.g., by a photon connecting the cat with observer’s eyes; defining a unique wavefunction that defines the perceived reality.

Concluding Remarks

Counterintuitive behavior of the physical systems, although described successfully by the rules of calculation of quantum mechanics, necessitated its various interpretations for an understanding of its epistemological underpinnings. Rather surprisingly, about the weakest among them, the Copenhagen interpretation; has been most widely accepted most of the times although at times, it has lost ground to the many worlds view. Another major interpretation, the pilot wave, has had its own following. The fact that determination of the “validity” of a scientific concept is reduced to winning popularity contest renders it non-scientific. In addition, these interpretations are untestable and thus, unfalsifiable rendering them scientifically unacceptable. By nature, these interpretations do not alter the essential contents of quantum mechanics; they juggle up the concepts to make the observed behavior of physical systems somehow palatable but they still remain quite tenuous.

Formulation of quantum mechanics incorporating the concepts of Weyl’s geometry adds something significant to the previous formulations by introducing the assigned gauge in it rendering the usually defined wavefunction an incomplete representation of reality; perceived reality is represented by the wavefunction together with the assigned gauge. This adjustment mitigates various bothersome arguments and explains the observed impact of the method of observation, observer, on the observation in a clear way: An act of observation is an assignment of gauge, which contains physically observable information. The impact of the assigned gauge is quantifiable and approximate calculations have shown it veracity warranting further investigations of this formulation.